程序设计基础

第五章函数

第5章函数

本章要点

函数的作用是什么? 如何确定函数功能?
怎样定义函数? 如何调用函数? 定义函数与声明函数有何区别?
什么是函数的参数? 怎样确定函数的参数?
在函数调用时，参数是如何传递数据的?
变量与函数有什么关系? 如何使用局部变量和全局变量?
什么是静态变量?

5.1 计算圆柱体积

例5-1. 输入圆柱体的高和半径，求圆柱体的体积$volume=\pi\times r^2\times h$，要求定义和调用函数cylinder(r, h)计算圆柱体积

5.1.1 程序解析

                        
#include<stdio.h>
double cylinder(double r, double h); /* 函数声明 */
int main()
{
    double height, radius, volumne;
    printf("Enter radius and height: ");
    scanf("%lf%lf", &radius, &height);
    volume=cylinder(radius, height);  /* 函数调用，将函数的返回值赋给volume */
    printf("Volume=%.3f\n", volume);
    return 0;
}
double cylinder(double r, double h)   /* 定义函数求圆柱体的体积 */
{
    double result;
    result=3.1415926*r*r*h;           /* 计算体积 */
    return result;                    /* 返回结果 */
}

函数调用是如何运行的?

5.1.2 函数的定义

函数是指完成一个特定工作的独立程序模块

库函数，由C语言系统提供定义，如scanf, printf等函数
自定义函数，需要用户自已定义，如计算圆柱体何种函数cylinder()

main()也是一个函数，C程序由一个main()或多个函数构成
程序中一旦调用了某个函数，该函数就会完成特定的计算，然后返回到调用它的地方

函数经过运算，会得到一个明确的运算结果，并需要回送该结果，如函数cylinder()返回圆柱的体积

函数定义(2)

函数定义形式:
/* 函数首部函数类型为返回值的类型，与return语句中表达式的类型一致 */
函数类型函数名(函数参数列表表)
{ /* 函数体 */
函数实现体
return 表达式; /* 将函数运算的结果送回调用该函数的地方 */
}

                        
/* 函数类型 double, 函数名 cylinder, 参数列表 double r和double h */
double cylinder(double r, double h) /* 函数首部 */
{   /* 函数体，写在一对大括号内 */
    double result;                 /* 函数内的局部变量 */
    result=3.1415926*r*r*h;        /* 计算圆柱体积 */
    return result;                 /* 返回运算结果，类型与函数类型一致 */
}

函数参数(形参)

                        
double cylinder(double r, double h)
{
    double result;
    result=3.1415926*r*r*h;
    return result;
}

函数的参数列表必须写成:类型1 参数1, 类型2 参数2, ......, 类型n 参数n
参数之间用逗号分隔，每个参数前面的类型都必须分别写明。比如上述函数中，参数double r, double h不能写成double r, h

5.1.3 函数的调用

定义一个函数后，就可以通过程序来调用这个函数
调用标准库函数时，在程序的最前面用#include命令包含相应的头文件
调用自定义函数时，程序中必须有与调用函数相对应的函数定义

函数调用的形式

函数调用的一般形式为: 函数名(实际参数列表)
对于实现计算功能的函数，函数调用通常会出现在两种情况中

赋值语句，如volume=cylinder(radius, height);
输出函数的结果，printf("%f", cylinder(radius, height));

函数调用的过程

程序执行从主函数main开始
如果遇到函数调用，暂停执行主函数，转到执行相应的函数
函数执行完毕后，返回主函数，再从原来主函数暂停的位置继续执行
如果调用函数执行过程中遇到return，则直接返回主函数

分析函数调用的过程

见DevC++

                        
#include<stdio.h>
double cylinder(double r, double h); /* 函数声明 */
int main()
{
    double height, radius, volumne;
    printf("Enter radius and height: ");
    scanf("%lf%lf", &radius, &height);
    volume=cylinder(radius, height);  /* 函数调用 8-->12  */
    printf("Volume=%.3f\n", volume);
    return 0;
}
double cylinder(double r, double h)   /* 参数列表赋值，实参->形参 */
{
    double result;                    /* 执行函数中的语句 */
    result=3.1415926*r*r*h;
    return result;                    /* 返回结果到调用的地方，第8行 */
}

参数传递

函数定义时的参数被称为形式参数，简称(形参)
double cylinder(double r, double h)
函数调用时的参数被称为实际参数，简称(实参)
volume=cylinder(radius, height);
参数传递，从实参-->形参，是单向传递

在参数传递过程中，实参将值复制给形参
形参和实参一一对应：数量一致，类型一致，顺序一致
形参: 是变量，用于接受实参传递过来的值
实参: 可以是常量、变量或表达式

函数结果返回

调用函数完成计算后，将运算结果返回给调用的函数，函数结果的返回形式一般有:
return 表达式;

return可用于返回函数运算的结果，也可用于终止调用函数的运行。函数只能返回一个值，如需要返回多个值，需采用其它方法实现

函数原型声明

函数声明，只写函数的首部，以分号结束，不包含函数体，即函数的实现部分
函数类型函数名(参数列表);
double volume(double r, double h);
void pyramid(int n);

函数必须先定义后调用，将主调函数放在被调函数的后面，就像变量先定义后使用一样
如果自定义函数在主调函数的后面，就需要在函数调用前，加上函数原型声明
函数声明，用于说明函数的类型和参数列表，以保证程序编译时能判断对该函数的调用是否正确

5.1.4 函数程序设计

例5-2. 计算五边形的面积

将一个五边形分割成3个三角形，输入这些三角形的7条边长，计算该五边形的面积。要求定义和调用函数area(x,y,z)计算边长为x,y,z的三角形面积

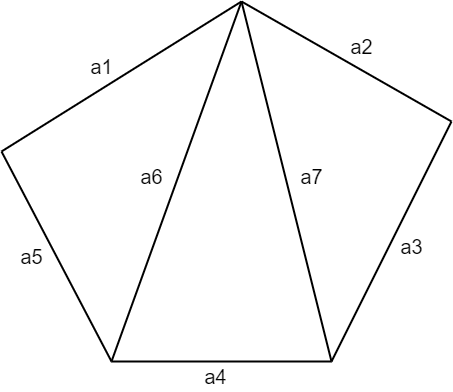
计算五边形面积源程序

                        
#include<stdio.h>
#include<math.h>
double area(double x, double y, double z);
int main()
{
    double a1, a2, a3, a4, a5, a6, a7, s;
    printf("Please input 7 side lengths in the order a1 to a7:");
    scanf("%lf%lf%lf%lf%lf%lf%lf", &a1, &a2, &a3, &a4, &a5, &a6, &a7);
    s=area(a1, a5, a6)+area(a4, a6, a7)+area(a2, a3, a7); /* 调用三次area函数计算面积 */
    printf("The area of the pentagon is %.2f\n", s);
    return 0;
}
/* 使用海伦-秦九韶公式计算三角形面积的函数 */
double area(double x, double y, double z)
{
    double p=(x+y+z)/2;
    return sqrt(p*(p-x)*(p-y)*(p-z));
}

自定义函数程序的优点

程序结构清晰，逻辑关系明确，程序可读性强
解决相同或相似问题时不用重复编写代码、可通过调用函数解决，减少代码量
利用函数实现模块化编程，各模块功能相对独立，利用“各个击破”降低调试难度

练习

练习. 判断奇偶数

定义一个判断奇偶数的函数even(n)，当n为偶数时返回1，否则返回0。利用该函数计算1-500之间所有偶数的和

                        
#include<stdio.h>
/* 判断奇偶性的函数 */
int even(int n)
{
    if(n%2==0)
        return 1;
    else
        return 0;
}

/* 求1-500之间所有偶数的和 */
int main()
{
    int i, sum=0;
    for(i=1; i<=500; i++)
    {
        if(even(i)==1)
            sum=sum+i;
    }
    printf("%d", sum);
    return 0;
}

判断完全平方数

例5-3. 判断完全平方数

定义一个判断完全平方数的函数isSquare(n)，当n为完全平方数时返回1，否则返回0，不允许使用数学库函数
如果n是完全平方数，则可以找到正整数m使$n=m^2$成立。在不使用函数sqrt()的情况下，我们可以判断一个数是否为完全平方数。例如，当n为完全平方数时，n可采用以下等差数列求和公式计算: $$ 1+3+5+7+\cdots+(2\times m-1)=m^2=n $$

判断完全平方数程序实现

                        
#include<stdio.h>
int isSquare(int n)
{
    int i;
    for(i=1; n>0; i=i+2)
    {
        n=n-i;
    }
    if(n==0)
        return 1; /* 是完全平方数返回1 */
    else
        return 0; /* 不是完全平方数返回0 */
}

int main()
{
    int n;
    printf("Enter n:");
    scanf("%d", &n);
    if(isSquare(n)==1)
        printf("%d is complete square number.\n", n);
    else
        printf("%d is not a complete square number.\n", n);
}

求最大公约数

例5-4. 求最大公约数

定义函数gcd(int m, int n)，计算m和n的最大公约数

辗转相除法(欧几里得算法)
1. temp=m%n
2. 若temp为0，返回n的值，否则转3.
3. m=n, n=temp, 转1继续

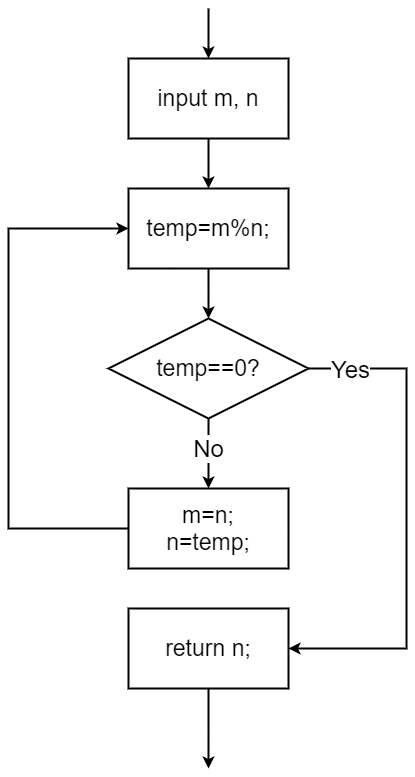
求最大公约数源程序

                        
#include<stdio.h>
int gcd(int m, int n)
{
    int r, temp;
    if(m<n)  /* 保证m比n大 */
    {
        temp=m;
        m=n;
        n=temp;
    }
    r=m%n;
    while(r!=0){
        m=n;
        n=r;
        r=m%n;
    }
    return n;
}
int main()
{
    int m, n;
    int g;
    printf("Enter two numbers m, n(m>n):");
    scanf("%d%d", &m, &n);
    g=gcd(m, n);
    printf("GCD of %d and %d is %d", m, n, g);
    return 0;
}

使用函数判断素数

例5-5. 使用函数判断素数

求100以内的全部素数，每行输出10个。素数是只能被1和自身整除的正整数，1不是素数，2是素数。
要求定义和调用函数prime(m)判断m是否为素数，当m为素数时返回1，否则返回0

使用函数判断素数源程序

                        
#include<stdio.h>
#include<math.h>
int prime(int m)
{
    int i, n, limit;
    if(m<=1)
        return 0;
    else if(m==2)
        return 1;
    else{
        limit=sqrt(m)+1;
        for(i=2; i<=limit; i++){
            if(m%i==0)
                return 0;
        }
    }
    return 1;
}
int main()
{
    int count, m;
    count=0;
    for(m=2; m<=100; m++){
        if(prime(m)!=0){
            printf("%6d", m);
            count++;
            if(count%10==0)
                printf("\n");
        }
    }
    printf("\n");
    return 0;
}

求$\pi$的近似值

示例. 使用函数求$\pi$的近似值

输入精度e，使用格雷戈里公式求$\pi$的近似值，精确到最后一项的绝对值小于e
$$ \frac{\pi}{4}=\frac{!}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots $$

求$\pi$的近似值源程序

                        
#include<stdio.h>
#include<math.h>
double funpi(double e)
{
    int denominator, flag;
    double item, sum;
    flag=1;
    denominator=1;
    item=1.0;
    sum=0;
    while(fabs(item)>=e){
        sum=sum+item;
        flag=-flag;
        denominator=denominator+2;
        item=flag*1.0/denominator;
    }
    sum=sum+item;
    return sum*4;
}
int main()
{
    double e, pi;
    printf("Enter e:");
    scanf("%lf", &e);
    pi=funpi(e);
    printf("pi=%f\n", pi);
    return 0;
}

5.2 数字金字塔

例5-6. 数字金字塔

输入一个正整数，输出n行数字金字塔。如当n=5时，输出的金字塔如下图所示

一行中的空格处理
一行中的数字显示
每一行的数字、空格处理

5.2.1 程序解析

                        
#include<stdio.h>
void pyramid(int n)   /* 函数定义 */
{
    int i, j;
    for(i=1; i<=n; i++){        /* 需要输出的行数 */
        for(j=1; j<=n-i; j++){  /* 输出每行左边的空格 */
            printf(" ");
        }
        for(j=1; j<=i; j++){     /* 输出每行的数字 */
            printf("%d ", i);    /* 注意每个数字后有空格 */
        }
        putchar('\n');           /* 换行 */
    }
}
int main()
{
    int n;
    printf("Enter n:");
    scanf("%d", &n);
    pyramid(n);
    return 0;
}

5.2.2 不返回运算结果的函数

void 函数名(参数列表)
{
函数实现体
return;
}

函数定义中，void表示函数不返回结果，但不能省略，否则函数类型会默认定义为int
返回类型为void的函数一般用于输出

不返回运算结果的函数定义

由于函数没有返回结果，函数调用不可能出现在表达式中，通常以独立的调用语句方式出现，如pyramid(5)
不返回结果的函数，在定义、调用、参数传递、函数声明上，思路与其它函数定义完全相同，只是函数类型为void
适用于将一些确定的、相对独立的程序功能包装成函数

主函数通过调用不同的函数，体现算法步骤
各步骤的实现由相应函数完成
简化主函数结构，以体现结构化程序设计思想

结构化程序设计思想

结构化程序设计(Structured Programming)是一种程序设计技术，C语言是结构化程序设计语言
结构化程序设计强调程序设计的风格和程序结构的规范化，提供清晰的结构

其基本思路是将一个复杂问题的求解过程划分为若干阶段，每个阶段要处理的问题都容易被理解和处理
按照自顶向下的方法对问题进行分析、模块化设计和结构化编码等3个步骤

自顶向下的分析方法

将大的复杂的问题分解为小问题后再解决

面对一个复杂的问题，首先进行上层(整体)的分析，按组织或功能将问题分解成子问题
如果子问题仍然十分复杂，再做进一步的分解，直到处理对象相对简单，容易处理为止
当所有的子问题都得到了解决，整个问题也就解决了

每一次分解都是对上一层问题进行细化和逐步求精，最终形成一种类似树形的层次结构，来描述分析的结果

学生成绩统计程序的层次结构图

学生成绩统计程序经分解后得到树状结构，每个模块均设计为独立的函数，整个程序通过调用函数实现

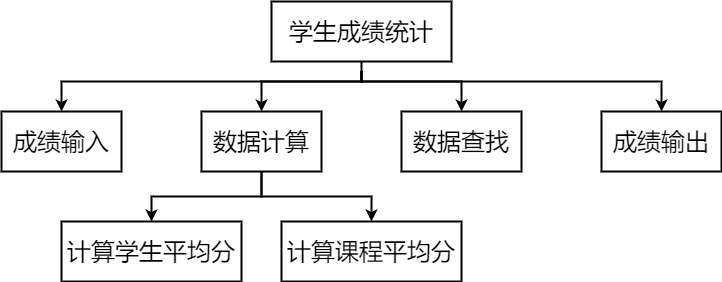
模块化设计

模块化设计是将模块组织成良好的层次系统

顶层模块调用其下层模块实现程序的完整功能
每个下层模块再调用更下层的模块，从而完成程序的每一个子功能
最下层的模块完成最具体的功能

遵循模块独立性的原则，即模块之间的联系应尽量简单，尽量保持模块之间的独立性
模块用函数实现
一个模块只完成一个指定的功能
模块之间只能通过带参数的函数进行调用

结构化编码的主要原则

经过模块化设计后，每一个模块都可以独立编码，编程时应选用顺序、选择和循环三种控制结构
对变量、函数、常量等命名时，要见名知意，有助于对变量含义或函数功能的理解
在程序中增加必要的注释，增加程序的可读性
要有良好的程序视觉组织，利用缩进格式控制页面排版
程序要清晰易懂，语句构造要简单直接
程序有良好的交互性，输入有提示，输出有说明

5.3 复数运算

例5-7. 计算两个复数的和与积

分别输入两个复数的实部与虚部，用函数实现计算两个复数的和与积

若两个复数分别为: c1=x1+y1i, c2=x2+y2i
则有
c1+c2=(x1+x2)+(y1+y2)i
c1*c2=(x1*x2-y1*y2)+(x1*y2+x2*y1)i

5.3.1 程序解析

                        
#include<stdio.h>
double result_real, result_imag; /* 全局变量，用于存放函数结果 */
void complext_add(double real1, double imag1, double real2, double imag2)
{
    result_real=real1+real2;
    result_imag=imag1+imag2;
}
void complex_prod(double real1, double imag1, double real2, double imag2)
{
    result_real=real2*imag1-real1*imag2;
    result_imag=real1*imag2+real2*imag1;
}
int main()
{
    double real1, real2, imag1, imag2; /* 两个复数的实部和虚部 */
    printf("Enter 1st complex number(real and imaginary):");
    scanf("%lf%lf", &real1, &imag1);
    printf("Enter 2nd complex number(real and imaginary):");
    scanf("%lf%lf", &real2, &imag2);   /* 分别输入两个复数的实部和虚部 */
    complex_add(real1, imag1, real2, imag2); /* 计算两个复数的和 */
    printf("addition of complex is %f+%fi\n", result_real, result_imag);
    complex_prod(real1, imag1, real2, imag2); /* 计算两个复数的积 */
    printf("product of complex is %f+%fi\n", result_real, result_imag);
    return 0;
}

5.3.2 全局变量和局部变量

局部变量

在函数内定义的变量(包括形式参数)，作用范围在本函数内部
定义在复合语句内的变量，作用范围在复合语句内部

全局变量

在函数以外定义的变量，不从属于任何一个函数，其作用范围是从定义处到源文件结束(包括各函数)

在复合语句中定义局部变量

                        
#include<stdio.h>
int main()
{
    int a;
    a=1;
    {              /* 复合语句开始 */
        int b=2;
        b=a+b;
        a=a+b;
    }              /* 复合语句结束 */
    printf("%d", a);
    return 0;
}

上述代码的输出是什么？如果将11行改为printf("%d", b);结果又如何？

全局变量定义

                        
#include<stdio.h>
int x;        /* 定义全局变量x */
int f()
{
    int x=4;  /* x是局部变量 */
    return x;
}
int main()
{
    int a=1;
    x=a;      /* 对全局变量x赋值 */
    a=f();    /* a的值为4 */
    {
        int b=2;
        b=a+b;    /* b的值为6 */
        x=x+b;    /* 全局变量运算, x的值为7 */
    }
    printf("%d %d", a, x);
    return 0;
}

若局部变量与全局变量同名，局部变量优先

变量作用范围示例

                            
int x=1;
void main()
{
    int a=2;
    //......
    {
        int b=3;    /* x=? a=? b=? */
        //......
    }
    f();
    //......        /* b=? */
}
int t=4;
void f()
{
    int x=5, b=6;   /* x=? a=? b=? t=? */
    //......
}
int a=7;      /* a=? b=? t=? x=? */

用函数实现财务现金记账

例5-8. 用函数实现财务现金记账

先输入操作类型: 1. 收入，2. 支出，0. 结束。再输入操作金额，计算现金剩余额，经多次操作直到输入操作类型为0时结束。要求定义并调用函数，其中现金收与现金支出分别用不同函数实现

分析：设变量cash保存现金余额值，由于它被主函数、现金收入与现金支出函数共用，任意使用场合其意义与数值都是明确且唯一的，因此将其设为全局变量

现金记账源程序

                        
#include<stdio.h>
double cash;   /* 定义全局变量，保存现金余额 */
void income(double number)  /* 定义现金收入函数 */
{
    cash=cash+number;       /* 改变全局变量cash的值 */
}
void expend(double number)  /* 定义现金支出函数 */
{
    cash=cash-number;       /* 改变全局变量cash的值 */
}
int main()
{
    int choice;
    double value;
    cash=0;      /* 初始金额为0 */
    printf("Enter operation choice(0-end, 1-income, 2-expend):");
    scanf("%d", &choice);
    while(choice!=0){  /* 若输入类型为0，结束循环 */

        if(choice==1 || choice==2){
            printf(“Enter cash value:");  /* 输入操作现金额 */
            scanf("%f", &value);
            if(choice==1)
                income(value);  /* 函数调用，计算现金收入 */
            else
                expend(value);  /* 函数调用，计算现金支出 */
            printf("Current cash: %.2f\n", cash);
        }
        printf("Enter operation choice(0-end, 1-income, 2-expend):");
        scanf("%d", &choice);
    }
    return 0;
}

关于全局变量和局部变量的思考

全局变量比局部变量自由度大，使用更方便?

对于规模较大的程序，过多使用全局变量会带来副作用，导致各函数间出现相互干扰。如果整个程序是由多个合作开发，各人都按自己的想法使用全局变量，相互的干扰可能会更严重
在变量使用中，应尽量使用局部变量，从某个角度看使用似乎受到了限制，但从另一个角度看，它避免了不同函数间的相互干扰，提高了程序质量

5.3.3 变量生命周期和静态局部变量

变量生命周期: 变量从定义开始分配存储单元，到运行结束存储单元被回收的整个过程
自动变量(auto)
全局变量: 从程序执行开始，到程序的结束，存储单元始终保持的变量

C程序存储分布示意图

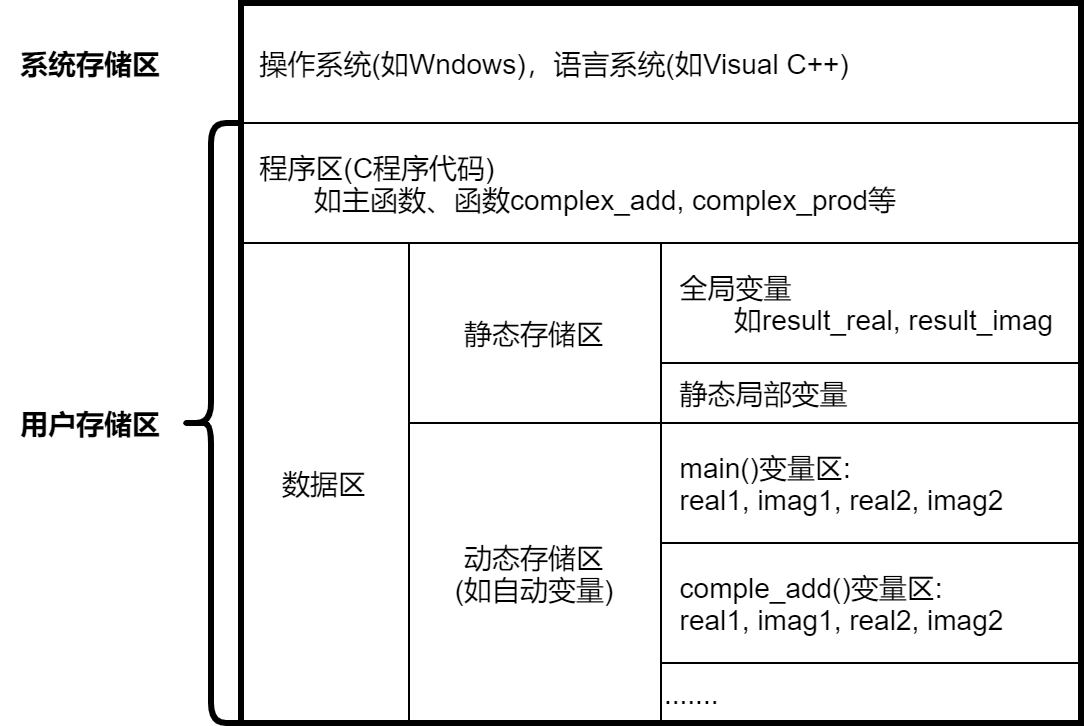
静态局部变量

static 类型名变量表

静态局部变量的作用范围是局部，但其生命周期是存在于全局

计算阶乘

例5-9. 计算阶乘

输入正整数n，输出1!~n!的值。要求定义并调用含静态变量的函数fact_s(n)计算n!

                        
#include<stdio.h>
double fact_s(int n)
{
    static double f=1;
    f=f*n;
    return f;
}
int main()
{
    int i, n;
    printf("Enter n:");
    scanf("%d", &n);
    for(i=1; i<=n; i++)
        printf("%3d!=%.0f\n", i, fact_s(i));
    return 0;
}

静态局部变量

自动变量如果没有赋初值，其存储单元中将是随机值
静态变量，如果定义时没有赋初值，系统将自动赋值为0
赋初值只在函数第一次调用时起作用，以后调用都按前一次调用后保留的值使用
静态局部变量受变量的作用范围限制，不能作用于其它函数，包括主函数

静态变量与全局变量

静态变量与全局变量均位于静态存储区，其共同点是生命周期贯穿整个程序执行过程
区别在于，作用范围不同，全局变量可作用于所有函数，静态变量只能用于所定义函数，而不能使用于其它函数

程序设计基础

第五章 函数

第5章 函数

本章要点

5.1 计算圆柱体积

5.1.1 程序解析

5.1.2 函数的定义

函数定义(2)

函数参数(形参)

5.1.3 函数的调用

函数调用的形式

函数调用的过程

分析函数调用的过程

参数传递

函数结果返回

函数原型声明

5.1.4 函数程序设计

计算五边形面积源程序

自定义函数程序的优点

练习

判断完全平方数

判断完全平方数程序实现

求最大公约数

求最大公约数源程序

使用函数判断素数

使用函数判断素数源程序

求$\pi$的近似值

求$\pi$的近似值源程序

5.2 数字金字塔

5.2.1 程序解析

5.2.2 不返回运算结果的函数

不返回运算结果的函数定义

结构化程序设计思想

自顶向下的分析方法

学生成绩统计程序的层次结构图

模块化设计

结构化编码的主要原则

5.3 复数运算

5.3.1 程序解析

5.3.2 全局变量和局部变量

在复合语句中定义局部变量

全局变量定义

变量作用范围示例

用函数实现财务现金记账

现金记账源程序

关于全局变量和局部变量的思考

5.3.3 变量生命周期和静态局部变量

C程序存储分布示意图

静态局部变量

计算阶乘

静态局部变量

静态变量与全局变量

第五章函数

第5章函数