计算机图形学

直线的扫描转换

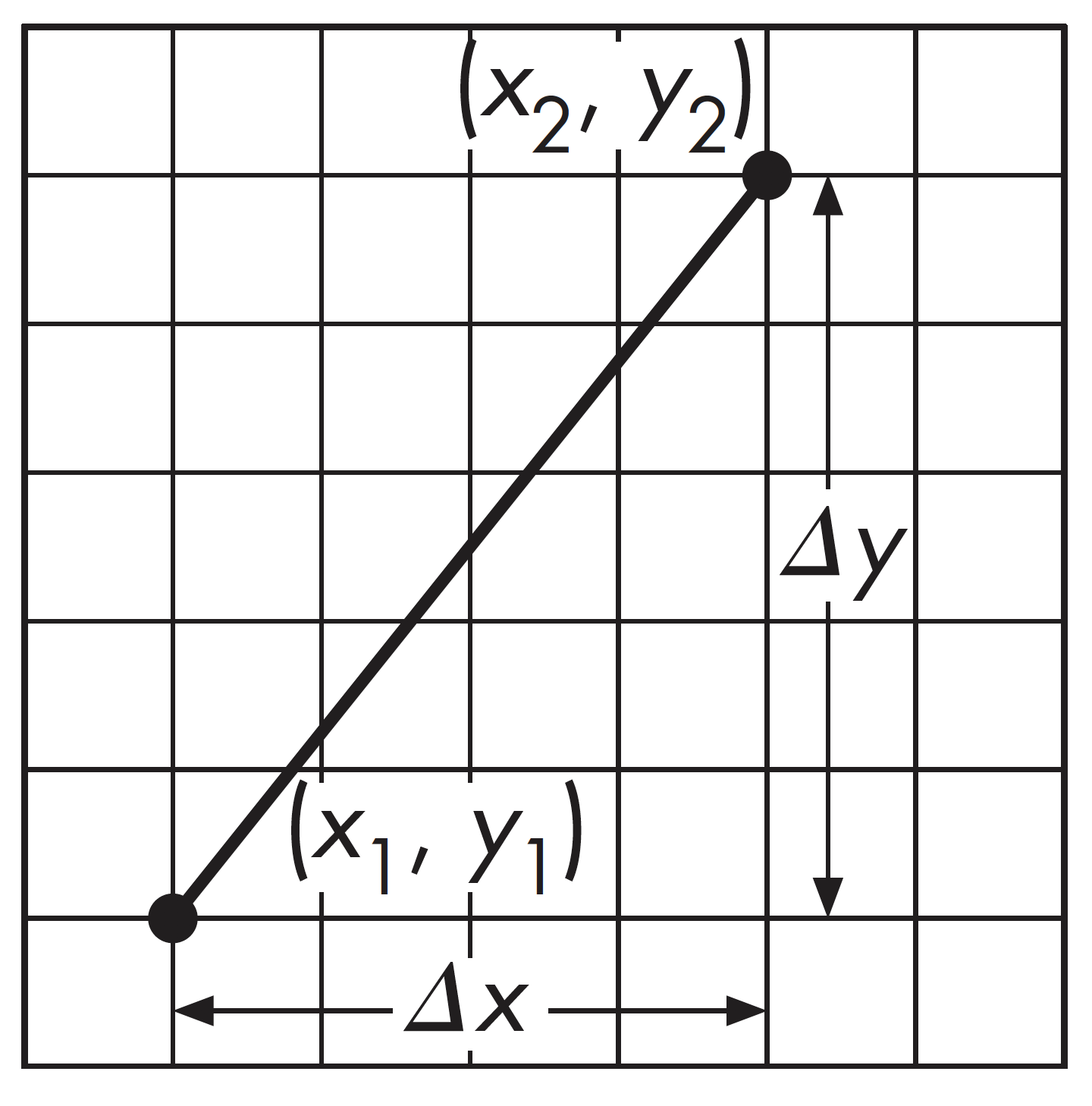
根据线段两个端点的坐标(通常是浮点数)，确定一组最佳逼近该线段的整数坐标像素点，并将这些像素点写入帧缓存的过程

• 假设有线段，两顶点坐标分别为$(x_1,y_1)$和$(x_2,y_2)$, 直线方程为$y=mx+h$，其中斜率为$m=\frac{y_2-y_1}{x_2-x_1} =\frac{\Delta x}{\Delta y}$
• 并假设已定义函数write_pixel用于绘制每个像素

DDA 算法 (Digital Differential Analyzer)

基本思想： 利用增量，在沿着扫描线$\Delta x=1$的方向上计算

假设 $0< m \le 1$，让 $x$ 每次步进 1 ($x_{k+1} = x_k + 1$)

则 $y$ 的增量为 $m$：

$y_{k+1} = y_k + m$

计算出的$y$值通常为浮点数，需要四舍五入取整，即$y_k=round(y_k)$

for(x=x1;x<=x2;x++){
	y+=m;
	write_pixel(x,round(y),line_color);
}                           
                        

DDA算法

DDA算法的主要思想是，对每一个$x$，计算距离其对应值最近的$y$值

对于斜率较大的线段，如$m >1$，$y$的增量较大，导致浮点数误差积累，影响最终效果

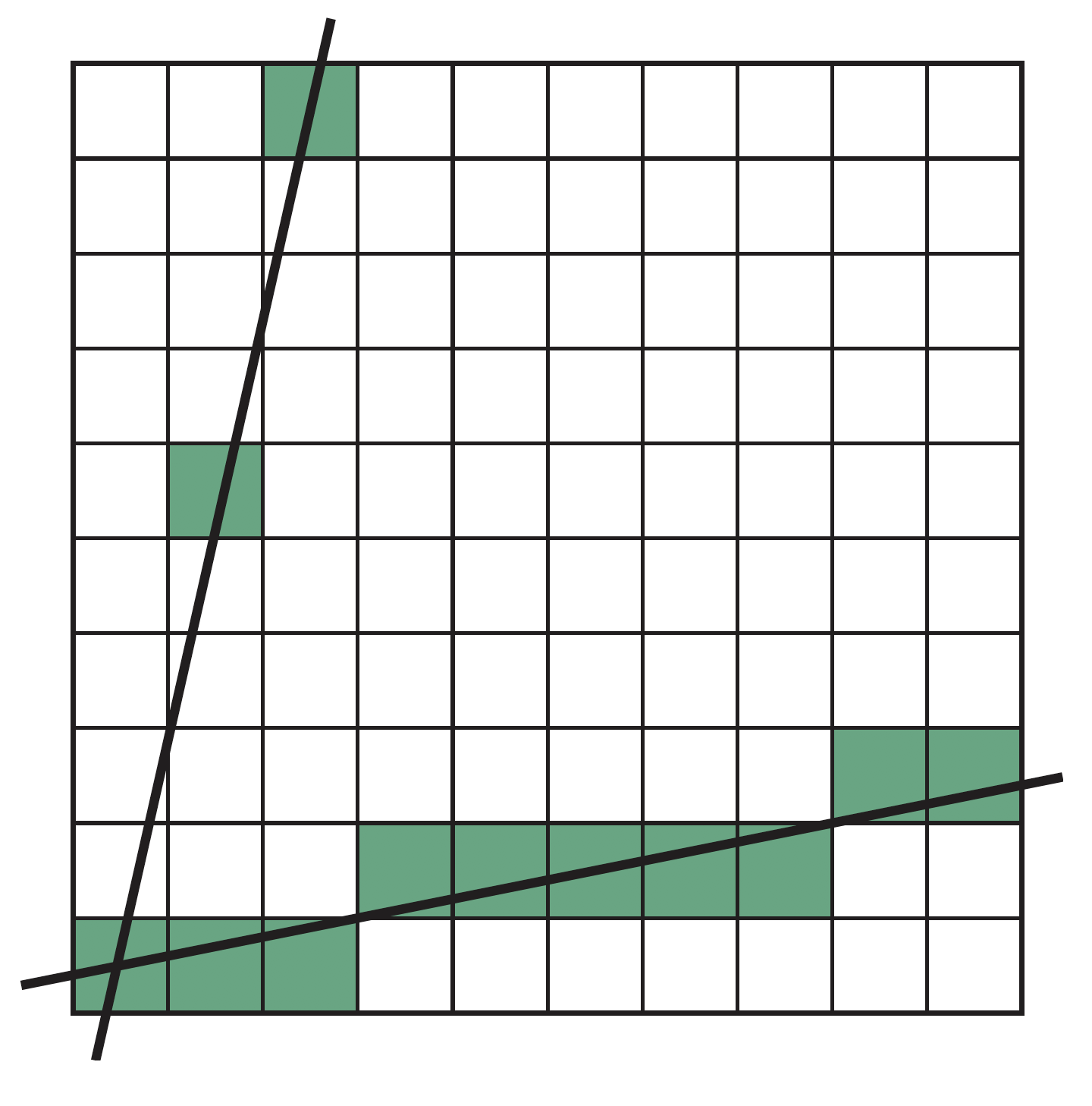
可利用对称性，原方法适用于$0\leq m \leq 1$的情况，当$m > 1$时，可交换$x$和$y$的角色，即对每个$y$，找到对应的$x$

DDA算法Demo

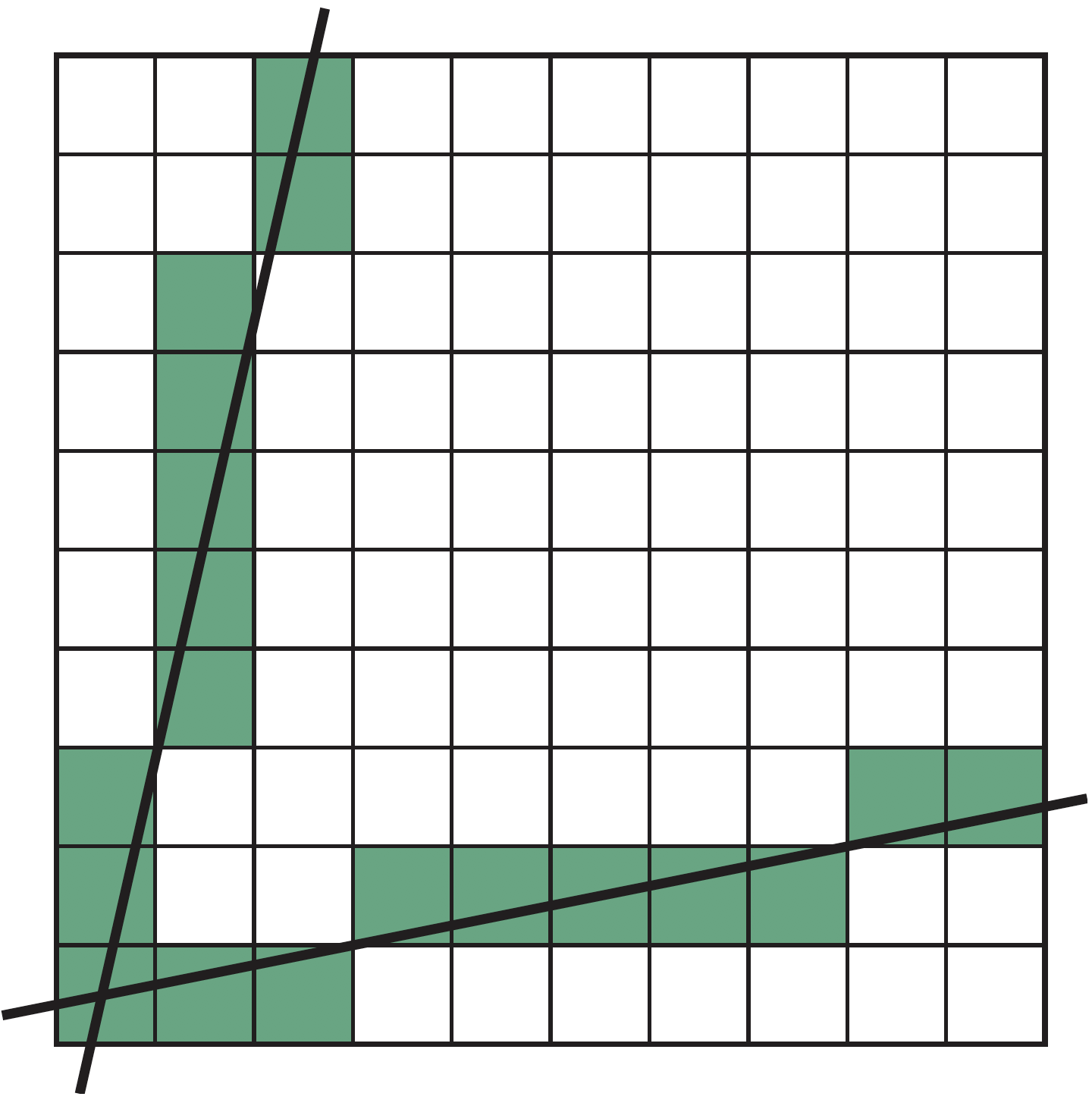
DDA 算法的优缺点

• 优点： 算法简单，利用了相邻像素的相关性
• 缺点：
  • 涉及浮点数加法和取整运算，速度较慢（在早期硬件上）
  • 浮点数累加可能导致精度误差积累

Bresenham画线算法

• DDA算法需要在每一步都执行浮点运算，在Bresenham算法中可避免浮点运算
• 算法运行可利用对称性先考虑$0\leq m\leq 1$的情况，其它情况可根据对称性进行计算
• 假设像素的中心位置为整数的一半
• 根据算法，如果从某一个特定像素开始绘制，下一个能够绘制的像素只有两种可能

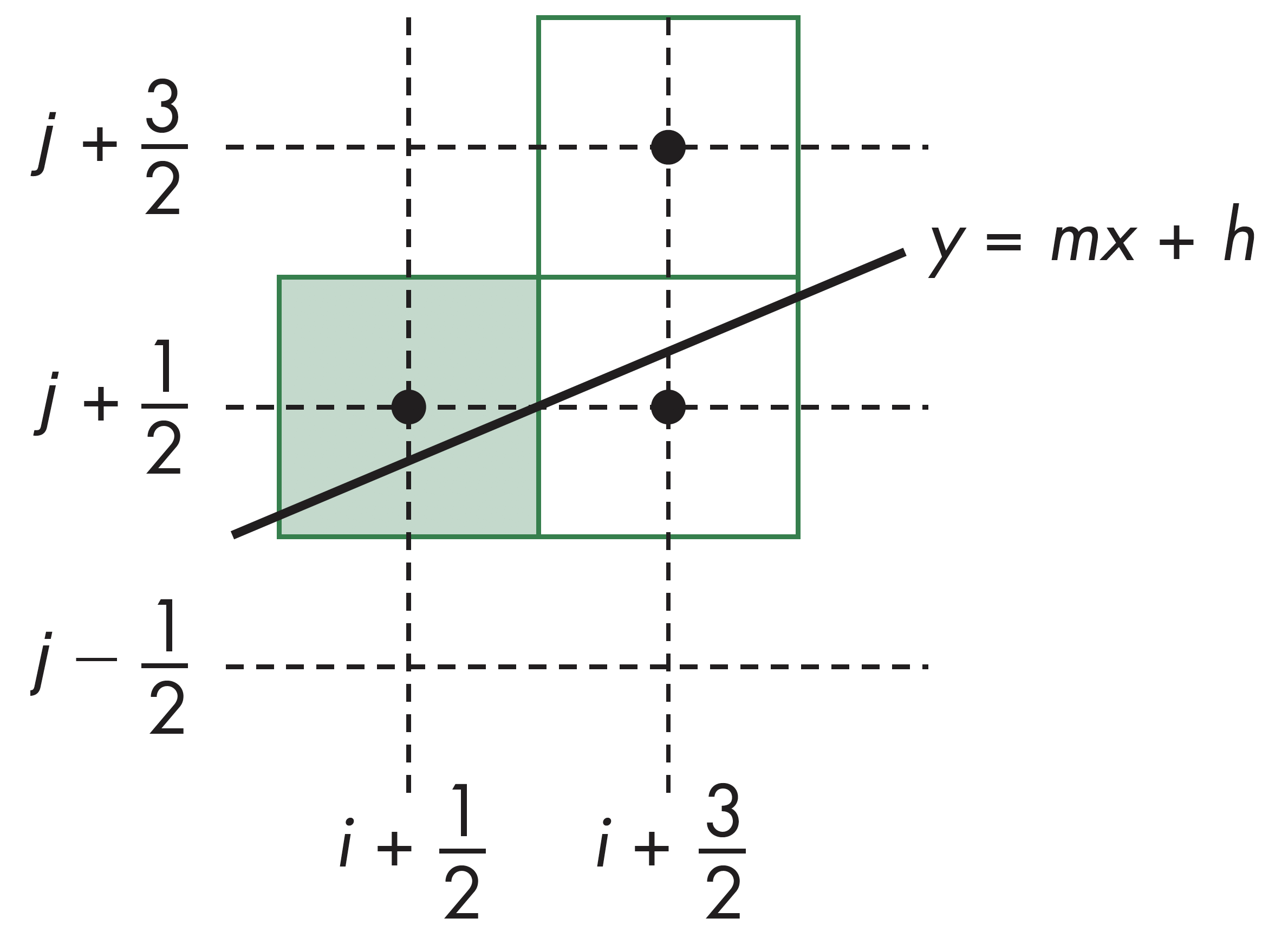
Bresenham画线算法

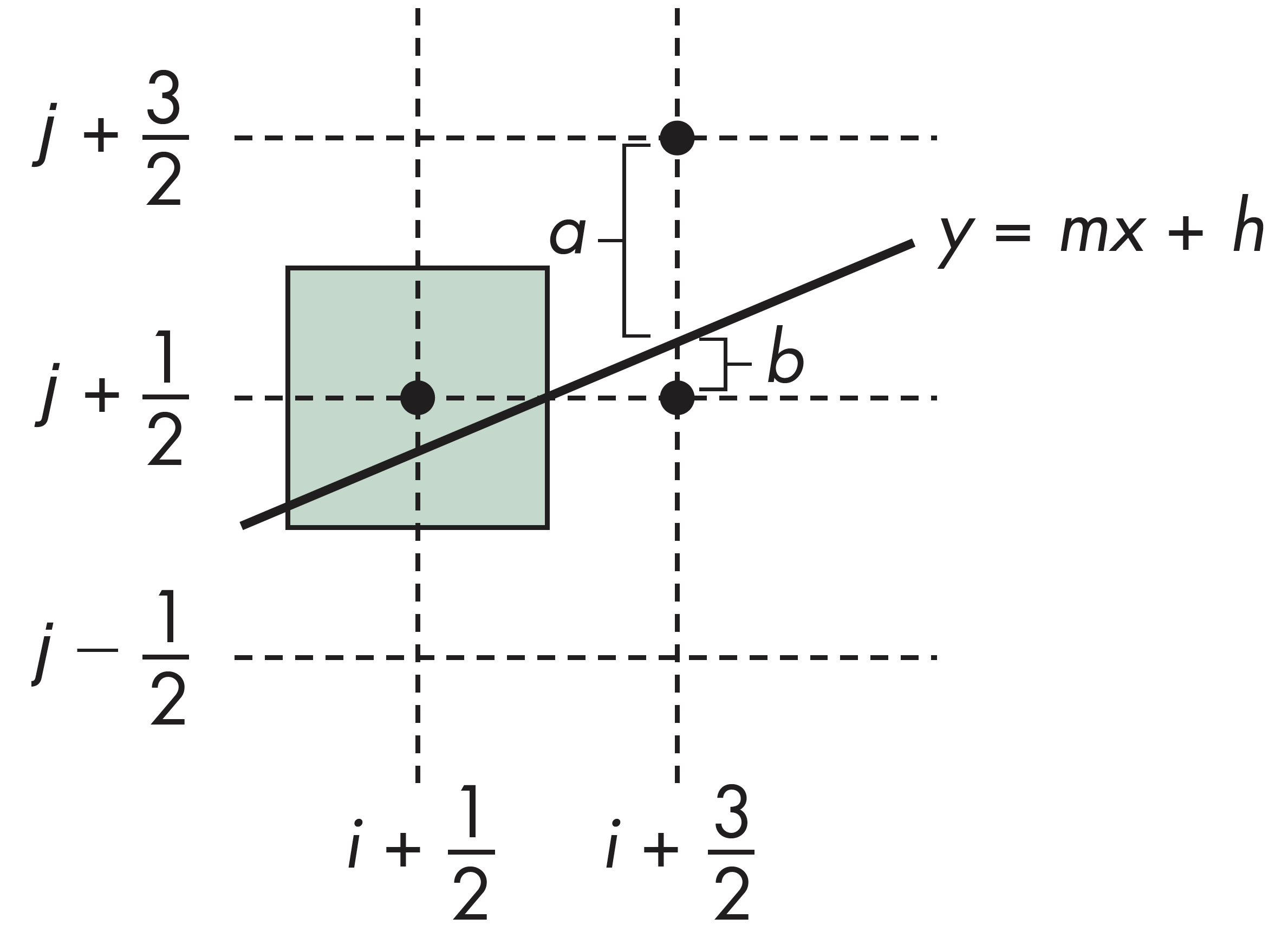
根据$p=\Delta_x(b-a)$的值，下一个候选点有两种情形：

• 若$p<0$，取下方像素，即下一个点为$(x_k+1, y_k)$
• 若$p\ge 0$，取上方像素，即下一个点为$(x_k+1, y_k+1)$

Bresenham画线算法

建立Bresenham画线算法的增量递推式提高计算$p$的效率。当$x=k$时，记为$p_k$，当$x=k+1$时，为$p_{k+1}$，有：

• $p_{k+1}=p_k+2\Delta_y$, $p_k\leq 0$
• $p_{k+1}=p_k+2(\Delta_y-\Delta_x)$, $p_k>0$
• $p_0=2\Delta_y-\Delta_x$

对每个$x$，只需一次整数加法和一次判断即可，在显卡核心上，只需要一条指令就能完成计算

Bresenham算法Demo

Bresenham 算法示例代码

void BresenhamLine(int x0, int y0, int x1, int y1) {
    int dx = abs(x1 - x0), dy = abs(y1 - y0);
    int p = 2 * dy - dx;
    int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);
    int x, y;
    // ... (处理不同象限和斜率，此处简化为 0 < m < 1 )
    if (x0 > x1) { x = x1; y = y1; x1 = x0; } 
    else { x = x0; y = y0; }
    
    setPixel(x, y);
    while (x < x1) {
        x++;
        if (p < 0)
            p += twoDy;
        else {
            y++;
            p += twoDyMinusDx;
        }
        setPixel(x, y);
    }
}
                    

圆的绘制

对圆心位于原点的圆，定义函数：$f(x,y)=x^2+y^2-r^2$

对任意一点$(x,y)$，有 $$ f(x,y)=\begin{cases} & f < 0, & if(x,y)在圆内 \\ & f = 0, & if(x,y)在圆弧上 \\ & f > 0, & if(x,y)在圆弧外 \end{cases} $$

圆的边界由函数$f(x,y)=0$确定

圆的绘制需要判断每个像素是否在圆内或圆外

如果直接采用方程式计算$y=\pm\sqrt{r^2-x^2}$, 因涉及开方运算，效率低且不均匀

圆的绘制

圆具有高度对称性。只要画出 $\frac{1}{8}$ 圆弧（例如 $0^\circ$ 到 $45^\circ$），就可以通过对称变换得到整个圆

因此，我们只需要计算 $0 \le x \le y$ 的部分

Bresenham算法画圆

类似Bresenham算法绘制直线，使用整数运算，根据圆弧上当前已占据的像素计算下一个像素的位置

• 当前像素为$x_k,y_k$时，下一个像素要么为$(x_k+1, y_k)$，或者是$(x_k+1, y_k-1)$
• 取哪个点，取决于这两个点中哪一个离圆弧更近
• 根据距离，同样可以建立递推式有： $$ p_{k+1}= \begin{cases} p_k+2x_{k+1}+1 & if p_k<0\\ p_k+2x_{k+1}+1-2y_{k+1} & if p_k>=0 \end{cases} $$ 其中，$2x_{k+1}=2x_k+2, 2y_{k+1}=2y_k-2$
• 当$p_k < 0$,取下一像素点为$(x_k+1,y_k)$，当$p_k \geq 0$，取下一像素点为$(x_k+1,y_k-1)$

圆的绘制

Bresenham画圆示例Demo

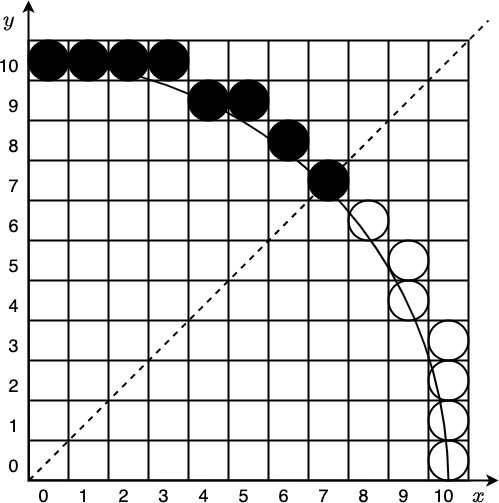
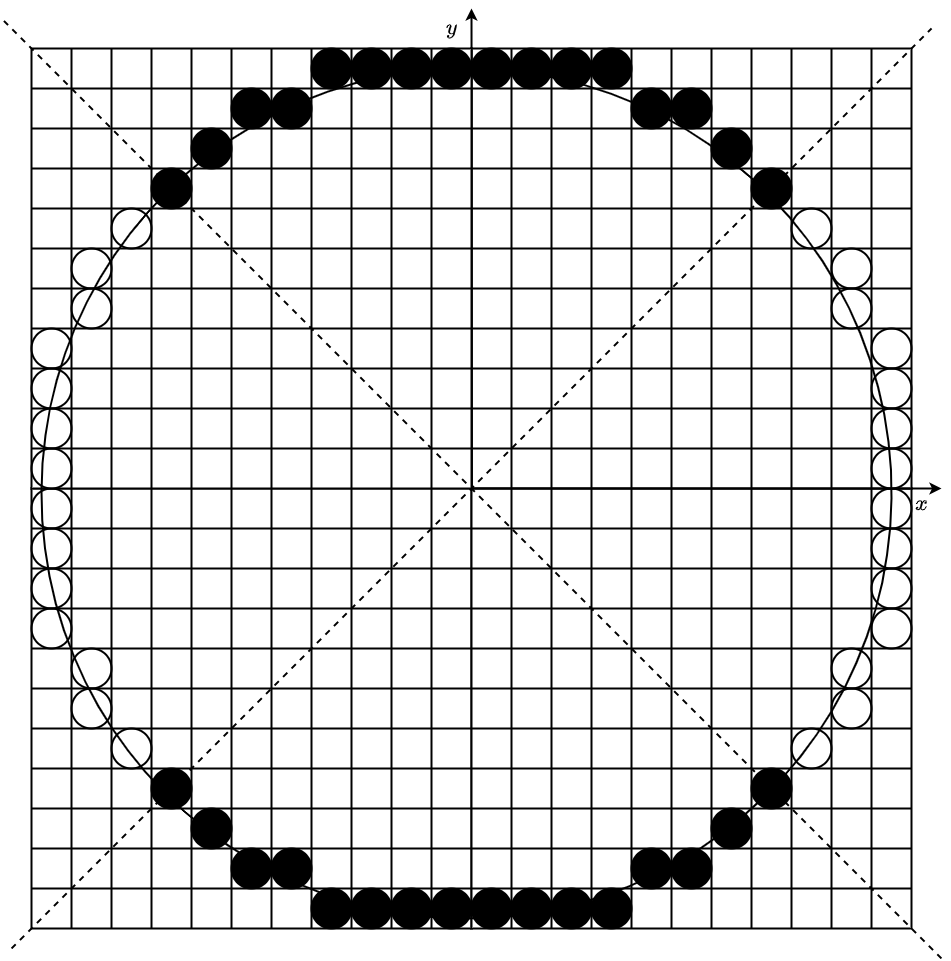
圆的绘制

Bresenham算法画圆的示例代码

void BresenhamCircle(int x0, int y0, int r) {
    int x = 0, y = r; // 从 (0,r) 开始
    int p = 1 - r;
    setPixel(x0 + x, y0 + y);
    setPixel(x0 - x, y0 + y);
    setPixel(x0 + x, y0 - y);
    setPixel(x0 - x, y0 - y);
    setPixel(x0 + y, y0 + x);
    setPixel(x0 - y, y0 + x);
    setPixel(x0 + y, y0 - x);
    setPixel(x0 - y, y0 - x);
    while (x < y) {
        if (p < 0)
            p += 2 * x + 3;
        else {
            p += 2 * (x - y) + 5;
            y--;
        }
        x++;
        setPixel(x0 + x, y0 + y);
        setPixel(x0 - x, y0 + y);
        setPixel(x0 + x, y0 - y);
        setPixel(x0 - x, y0 - y);
        setPixel(x0 + y, y0 + x);
        setPixel(x0 - y, y0 + x);
        setPixel(x0 + y, y0 - x);
        setPixel(x0 - y, y0 - x);
    }
}

随堂测试(1)

随堂测试(2)

随堂测试(3)