计算机图形学
第五章(2) 光照与着色
李懿
医学技术与信息工程学院
浙江中医药大学
绘制的“真实感”
从线框到逼真的渲染,赋予物体“真实感”,关键因素是什么?
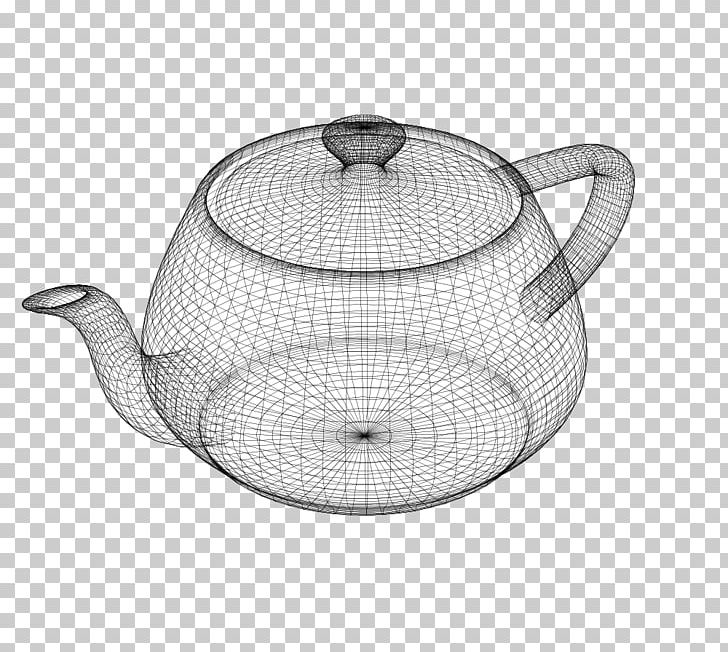

需要:光、材质、观察点、表面朝向(法向量)
局部光照模型
将光、材质、观察点、表面朝向结合在一起,模拟真实世界的光照,需要建立一个光照模型
最经典、应用最广泛的局部光照模型:
其主要思想是,利用几个简单的部分模拟复杂的光照现象,在计算效率和真实感之间取得了平衡
学习目标
- 阐述Phong光照模型的基本原理
- 比较Phong光照模型的三个分量的异同:环境光、漫反射光和镜面反射光
- 推导Phong光照模型的数学表达式及计算方法
- 解释Blinn-Phong模型与比较其与普通Phong模型的优势
Phong光照模型简介
Phong光照模型是由越南裔计算机图形学家裴祥风(Bùi Tường Phong)在1975年提出的
是一种局部光照模型,广泛应用于实时渲染
通过模拟光与物体表面的相互作用,产生真实感的视觉效果
Phong光照模型的组成
Phong光照模型将光照效果分解为三个独立的分量:

最终的光照效果是这三种光照分量的叠加
Phong模型的数学表达式
Phong模型的计算公式:
$I = I_{ambient}+I_{diffuse}+I_{specular}$
其中:
- $I_{ambient}$:环境光分量
- $I_{diffuse}$:漫反射光分量
- $I_{specular}$:镜面反射光分量
向量表示
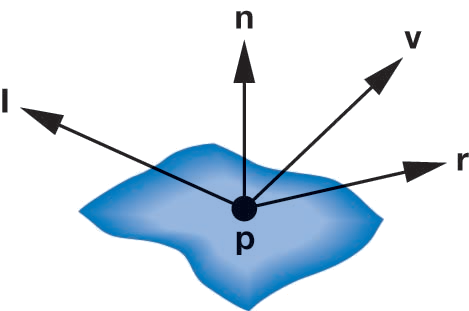
- $\vec{n}$:表面法向量(Normal vector)
- $\vec{l}$:指向光源的单位向量(Light vector)
- $\vec{v}$:指向观察者的单位向量(View vector)
- $\vec{r}$:全反射向量(Reflection vector)
可通过这四个向量计算得到三种分量
环境光分量 (Ambient Light)

环境光是光源和环境中物体进行多次交互后的结果,是对间接光照的简化模拟
假设来自所有方向的光照强度相等
不考虑光源位置和物体表面朝向
环境光强度和颜色取决于光源的颜色和物体的材质属性
计算公式:
$I_{ambient}=k_{a}I_{a}$
- $k_a$:环境光反射系数(材质属性)
- $I_a$:环境光强度
环境光的意义


环境光确保了场景中没有完全黑暗的区域,模拟了现实世界中光线的多次散射
虽然不真实,但是能实现简单有效的近似模拟
朗伯面
朗伯面(Lambertian Surface),一种理想的漫反射表面,光线均匀地向各个方向散射
反射光强度与入射光在垂直方向上的强度呈线性关系,即
- 反射光强度与$\cos{\theta}$呈线性关系
- 若向量已正则化,有$\cos(\theta)=\vec{l}\cdot\vec{n}$
- 可对三个颜色分量分别计算反射量,反射系数分别为$k_r, k_g, k_b$
漫反射光分量 (Diffuse Light)

漫反射模拟光线在粗糙表面上的反射
基于朗伯定律(Lambert's Law):反射光强度与入射光和表面法线夹角的余弦成正比
计算公式:
$I_{diffuse}=k_{d}I_{d}(\vec{n}\cdot\vec{l})$
- $k_d$:漫反射系数(材质属性)
- $I_d$:光源强度
- $\vec{n}·\vec{l}$:法向量与光源方向的点积(余弦值)
漫反射的特点
- 当$\vec{n}\cdot\vec{l}>0$时,表面接收光照
- 当$\vec{n}\cdot\vec{l}\leq 0$时,表面背向光源,不接收光照
- 漫反射光与观察者位置无关
- 漫反射决定了物体的基本明暗变化,提供了物体的形状感
漫反射适合表现如纸张、布料、墙壁等不光滑表面的光照效果
理想反射面
- 法向量由局部方向决定
- 光线入射角等于反射角
- 三个向量共面,包括入射光向量、法线向量和全反射向量
$$ \vec{r}=2(\vec{l}\cdot\vec{n})\vec{n}-\vec{l} $$

高光表面
- 大多数平面既非理想的漫反射表面,也非理想的镜面(即理想全反射面)
- 平滑表面会在接近于镜面反射方向反射入射光,形成高光

高光反射建模
- Phong模型以一个变量$I_{specular}$表示反射光强度
- 当观察者与全反射角之间的角度增大时,反射光强度会减小,即有$I_{specular}\sim k_sI_s\cos^{\alpha}({\phi})$
- $I_{specular}$表示反射强度
- $k_s$为光反射系数,其值介于0和1之间,表明有多少光被反射
- $I_s$为入射光强度
- $\cos^{\alpha}({\phi})$为Phong模型中定义的闪光系数
- $\phi$为观察者与全反射方向之间的夹角

镜面反射光分量 (Specular Light)

镜面反射模拟光线在光滑表面上的反射
产生高光效果,与观察者位置相关
计算公式:
$I_{specular}=k_{s}I_{s}(\vec{r}\cdot\vec{v})^{\alpha}$
- $k_s$:镜面反射系数(材质属性)
- $I_s$:光源强度
- $\vec{r}\cdot\vec{v}$:反射向量与视线向量的点积
- $\alpha$:光泽度(shininess),控制高光大小
光泽度(Shininess)
- 当$\alpha$无限趋近于正无穷时,对应于镜面材质
- 当$\alpha$值界于100到200之间时,对应于较为金属材质
- 当$\alpha$值界于10到50之间时,对应于塑料材质

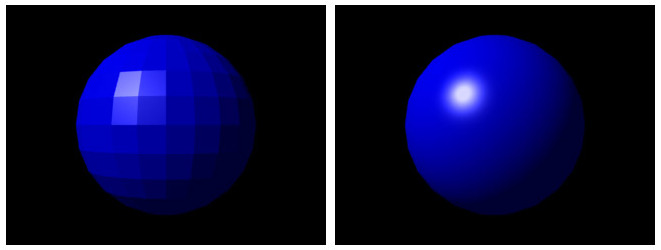
光泽度(Shininess)的影响

低光泽度

中光泽度

高光泽度
- 光泽度α越大,高光区域越小越集中,表面越光滑
- 光泽度α越小,高光区域越大越分散,表面越粗糙
距离因子
在现实世界中,光照强度会随着距离增加而衰减
其强度衰减与距离平方的倒数相关,因此,衰减因子为
$$att = \frac{1}{k_1+k_2 d+k_3 d^2}$$
其中$d$为光源到表面点的距离,$k_1$、$k_2$、$k_3$分别为常数项、线性项和二次项的衰减系数
将衰减因子应用到漫反射和镜面反射分量中
Phong模型计算式
- 将前述各分量相加,得到Phong模型的计算式,对于每一个光源,有 $$ I = k_a I_a +\frac{1}{k_1+k_2 d+k_3 d^2}\cdot\left( k_d I_d (\vec{n}\cdot\vec{l}) + k_s I_s (\vec{r}\cdot\vec{v})^{\alpha}\right) $$
- 如果场景中有多个光源,将所有光源的漫反射和镜面反射分量相加,即可得到完整的光照计算式,有 $$ I = k_a I_a +\sum_{i=1}^n\left(\frac{1}{k_1+k_2 d+k_3 d^2}\cdot\left( k_d I_d (\vec{n}\cdot\vec{l}) + k_s I_s (\vec{r}\cdot\vec{v})^{\alpha}\right)\right) $$

光源和材质
- Phong模型中,可对每个光源单独计算各分量
- 每个光源都有独立的漫反射、高光反射和环境光分量,可灵活计算调整,但这种模型并不符合物理实际
- 每种分量又可进一步分解成红、绿、蓝三种颜色分量,因此每个光源都有$I_{dr}, I_{dg}, I_{db}, I_{sr}, I_{sg}, I_{sb}, I_{ar}, I_{ag}, l_{ab}$九个分量
- 对于物体的材质,也与光源性质相类似,分别对应于三种光源三种颜色分量的吸收性质,有$k_{dr}, k_{dg}, k_{db}, k_{sr}, k_{sg}, k_{sb}, k_{ar}, k_{ag}, k_{ab}$
- 除外,不同的材质的光泽度系统$\alpha$也不同
- 因此,可对每个光源每种材质独立进行计算后再相加
改进Phong模型
在Phong模型计算中,对于镜面反射分量的计算,需要计算每个顶点的观察者向量,以及全反射向量,计算量大
Jim Blinn于1977年提出了一种对Phong模型的优化改进,称为Blinn-Phong模型
Blinn-Phong模型引入半路向量(Half Vector)替代全反射向量,提高计算效率
$$ \vec{h}=\frac{(\vec{l}+\vec{v})}{|\vec{l}+\vec{v}|} $$

改进Phong模型的计算
将Phong模型中$(\vec{v}\cdot\vec{r})^{\alpha}$替代为$(\vec{n}\cdot\vec{h})^\beta$,其中$\beta$的值根据光泽度$\alpha$的值设定,一般$\beta\approx 4\alpha$
如果所有向量均共面,则半路角为$\vec{r}$和$\vec{v}$夹角的一半,即$\psi=\phi/2$
Phong vs Blinn-Phong
Blinn-Phong模型的优势:
- 计算效率更高(避免了反射向量的计算)
- 在掠射角度(视线几乎平行于表面)时表现更好
- 在现代图形API和着色器中广泛使用
Phong模型的局限性
- 简化了真实世界的光照交互
- 不能模拟复杂的光照效果:
- 次表面散射
- 光的色散
- 光的衍射
- 不考虑物体间的光线传递
- 不支持真实的阴影生成

尽管有局限性,Phong模型因其简单高效的特点,仍然在实时渲染中广泛应用
Phong模型示例

题目一 (选择题)
在Phong光照模型中,以下哪个分量与观察者的位置无关?
- A. 环境光分量
- B. 漫反射分量
- C. 镜面反射分量
答案: A. B
解析: 在Phong光照模型中,漫反射分量仅依赖于光线方向与表面法线的夹角,与观察者位置无关。漫反射计算公式为 Idiffuse = kd × Id × (N·L),其中不包含视线向量V。环境光分量也与观察者位置无关。镜面反射分量与观察者位置密切相关,因为它依赖于反射向量和视线向量的夹角。
题目二 (单选题)
Blinn-Phong模型相比原始Phong模型的主要优化是什么?
- A. 增加了环境光计算的准确性
- B. 改进了漫反射计算方法
- C. 使用半路向量(Half Vector)替代反射向量,提高计算效率
- D. 添加了光照衰减因子
答案: C
解析: Blinn-Phong模型的主要优化是使用半路向量(Half Vector)H替代反射向量R来计算镜面反射。半路向量是光源方向L和视线方向V的归一化平均值:H = (L + V) / |L + V|。这种方法避免了计算反射向量的开销,提高了计算效率,并在某些情况下(如掠射角)产生更好的视觉效果。Blinn-Phong模型的镜面反射计算使用(N·H)α'替代了Phong模型中的(R·V)α。
题目三 (问答题)
一个3D场景中有一个红色的塑料球和一个银色的金属球,它们在相同的光照条件下呈现出不同的视觉效果。请结合Phong光照模型的三个分量,解释如何通过调整材质参数来区分这两种不同材质的球体。具体说明哪些参数应该如何设置,以及为什么这些设置能够产生塑料和金属的视觉差异。
答案解析:
- 材质参数差异:
要区分红色塑料球和银色金属球,需要调整以下Phong模型参数: - 漫反射系数(kd):
- 红色塑料球: 设置较高的红色通道漫反射系数(kd,r),较低的绿色和蓝色通道系数。塑料材质主要通过漫反射呈现颜色,因此kd应该占主导。
- 银色金属球: 设置较低的漫反射系数,且RGB三个通道值接近(灰色调)。金属材质的漫反射较弱,颜色主要通过镜面反射呈现。
- 镜面反射系数(ks):
- 红色塑料球: 设置较低的镜面反射系数,且通常为白色(RGB值相等)。塑料的高光通常是白色的,与物体本身颜色无关。
- 银色金属球: 设置较高的镜面反射系数,且RGB值接近(银色调)。金属的高光通常继承了金属本身的颜色。
- 光泽度(α):
- 红色塑料球: 设置中等的光泽度值(如α=16~32)。塑料表面虽然有光泽,但不如金属那么锐利集中。
- 银色金属球: 设置较高的光泽度值(如α=64~128或更高)。金属表面通常非常光滑,产生锐利集中的高光。
- 环境光反射系数(ka):
两者的环境光系数可以设置相似,但应与各自的漫反射系数保持一致的颜色比例。 - 视觉效果解释:
这些参数设置的结果是:红色塑料球会呈现出均匀的红色表面,带有较为柔和的白色高光;而银色金属球则会显示出强烈的镜面反射效果,高光区域锐利且带有金属本身的色调,整体看起来更加"闪亮"和"反光"。这符合我们在现实世界中对这两种材质的视觉感知。
课堂总结
- Phong光照模型是一种经典的局部光照模型,由环境光、漫反射光和镜面反射光三个分量组成
- 环境光分量模拟间接光照,与表面朝向和观察位置无关
- 漫反射分量基于朗伯定律,与表面朝向相关但与观察位置无关
- 镜面反射分量产生高光效果,与表面朝向和观察位置都相关
- Blinn-Phong模型通过使用半路向量优化了计算效率,在现代图形应用中广泛使用