计算机图形学

第四章(2) 观察

如何”实现”投影

想象一下，在无限大的三维世界中，该如何告诉计算机，你想“看”哪里？

需要定义一个虚拟相机(Virtual Camera)

学习目标

  • 流水线中的位置：理解视图和投影变换在图形渲染流水线中的位置和作用
  • 定义相机：掌握使用视点(Eye)、目标点(At)和上方向(Up)向量设置相机
  • 视图变换：理解视图变换的目的，及其“变换世界，而非相机”的核心思想
  • 视图矩阵：理解视图矩阵$M_{view}$的推导过程

如何简化计算

假设你要拍摄一座巨大的山脉

从“数学”的角度，下面哪种方式的坐标系设置更“简单”？

A. 山脉不动，相机动

保持山脉不动，你带着相机到处移动，寻找最佳角度和位置

为每个点计算相对于最佳位置相机的投影

B. 相机不动，山脉动

将相机固定在某个位置，以这个位置为原点，你移动和旋转整个地球，通过山脉移动，让山脉对准相机镜头，找到最佳角度和位置

相机位置“始终”在原点，并且朝向$-Z$方向

答案：B

将相机标准化，能够用一个统一的、简单的投影公式处理所有的物体，简化投影计算，这就是视图变换的核心思想

视图变换

一个顶点从模型到最终显示在屏幕上，需要经历一系列坐标系的变换

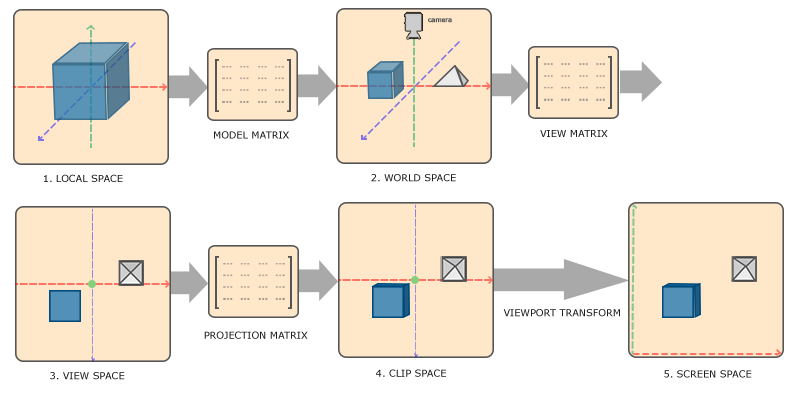
坐标系变换
  1. 模型变换 (Model Transformation)：将物体从局部坐标系变换到世界坐标系
  2. 视图变换 (View Transformation)：将世界坐标系中的物体变换到相机坐标系
  3. 投影变换 (Projection Transformation)：将三维场景投影到二维平面
  4. 裁剪 (Clipping)：去除视野外的部分
  5. 屏幕映射 (Screen Mapping)：将规范化设备坐标映射到屏幕坐标

视图变换

目标：将位于世界坐标系任意位置的相机，变换到相机坐标系(View Space)的原点，即标准观察位置，并使其看向$-Z$轴方向，并保持$+Y$向上

视图变换

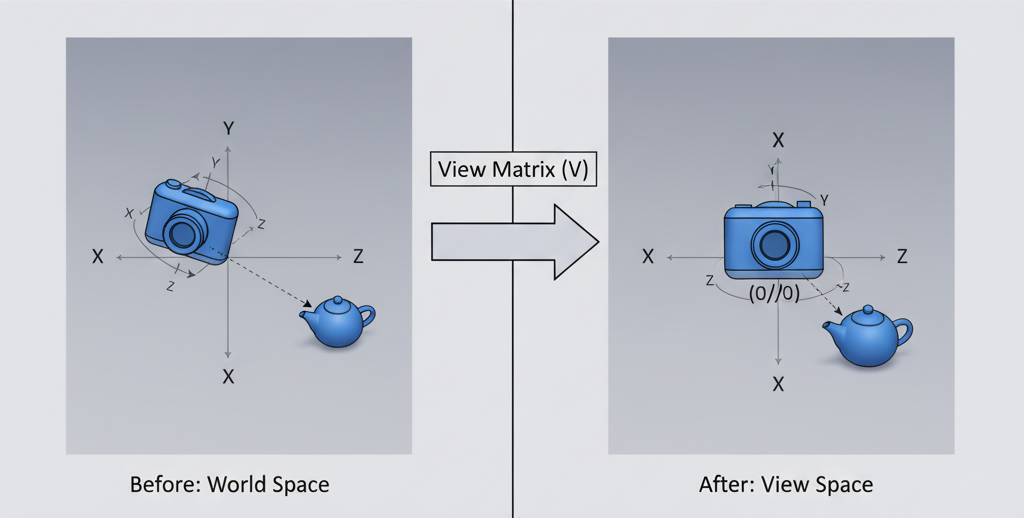
对整个场景施加一个与相机变换相反的逆变换实现

这个逆变换矩阵就是视图矩阵(View Matrix)$M_{view}$

定义相机

关键是构建相机坐标系(View Space)，即要找到构建相机坐标系的三个正交基向量$(n, u, v)$

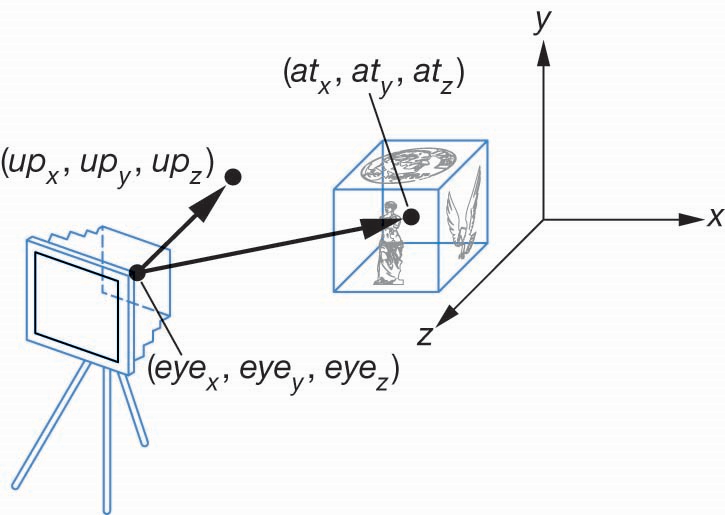
相机设置的三要素：

  • $E$(eye position)：相机在世界坐标系中的位置
  • $A$(at)：相机看向的目标点
  • $\vec{u}$(up)：定义相机“头顶”朝向的上方向，用于确定相机的旋转，一般取$(0,1,0)$
相机定义

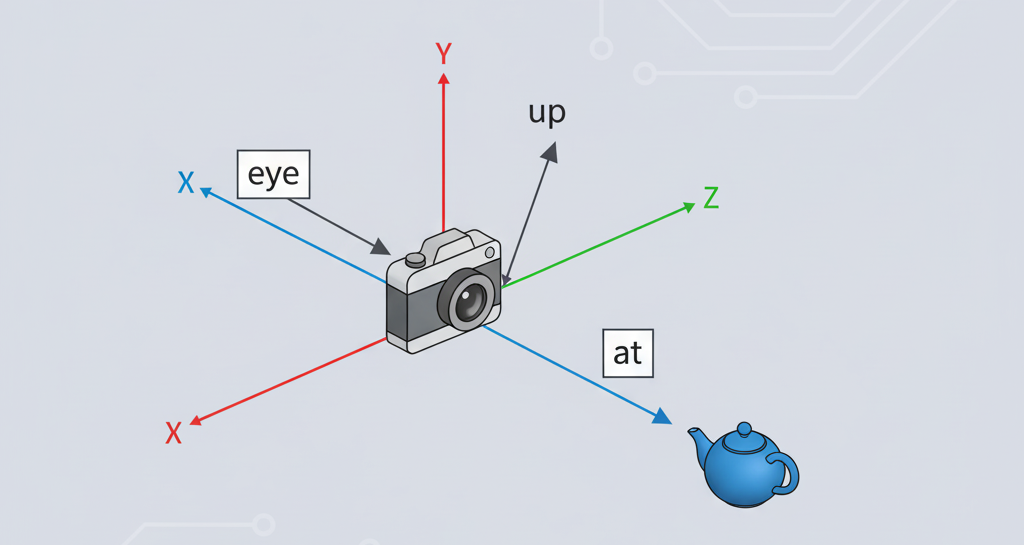
构建相机坐标系(View Space)

从相机三要素计算相机坐标系的三个正交基向量

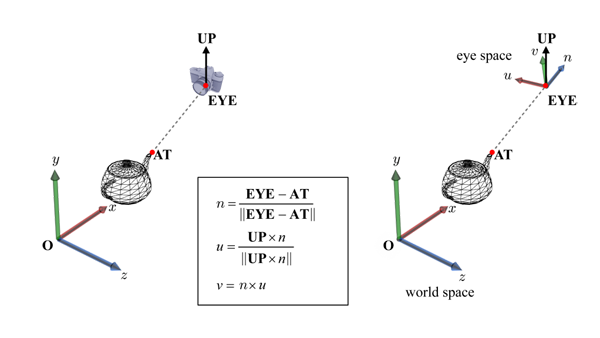
相机坐标系

$Z$轴（指向观察者）：$\vec{n}$，$X$轴（指向右方）：$\vec{u}$，$Y$轴（指向上方）：$\vec{v}$

相机变换

相机初始化时，位置位于原点，指向$Z$轴负方向

若要同时看到$Z$轴正方向和负方向的物体对象

  • 沿$Z$轴正方向移动相机，即改变相机坐标
  • 沿$Z$轴负方向移动物体，即改变物体坐标

这两者成像结果是等价的

移动相机与移动物体方法一样，可以采用任意旋转和平移序列将相机放置到适当位置

构建视图矩阵$M_{view}$

视图矩阵$M_{view}$包含两部分：

1. 平移($T$)：将相机位置$E$平移到原点

$T = \begin{bmatrix} 1 & 0 & 0 & -e_x \\ 0 & 1 & 0 & -e_y \\ 0 & 0 & 1 & -e_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$

2. 旋转($R$)：将相机坐标系$(u,v,n)$旋转至与世界坐标系$(x,y,z)$重合

$R = \begin{bmatrix} u_x & u_y & u_z & 0 \\ v_x & v_y & v_z & 0 \\ n_x & n_y & n_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

视图矩阵$M_{view}=RT$，这个过程通常被封装在lookAt函数中

lookAt函数

lookAt函数 lookAt(eye, at, up) 

lookAt(eye, at, up) {
    // 计算相机坐标系的三个基向量
    let g = normalize(subtract(at, eye));
    let t = normalize(cross(up, g));
    let u_prime = normalize(cross(g, t));
    
    // 构建旋转矩阵
    let R = mat4(
        t[0], u_prime[0], -g[0], 0,
        t[1], u_prime[1], -g[1], 0,
        t[2], u_prime[2], -g[2], 0,
        0, 0, 0, 1
    );
    
    // 构建平移矩阵
    let T = translate(-eye[0], -eye[1], -eye[2]);
    
    // 返回视图矩阵
    return mult(R, T);
}


var eye=vec3(1.0, 1.0, 1.0);
var at=vec3(0.0, 0.0, 0.0);
var up=vec3(0.0, 1.0, 0.0);
var mv=lookAt(eye, at, up);

lookAt Demo

课堂测试

  1. 定义一个虚拟相机需要哪三个核心向量？

    视点 (Eye), 目标点 (At), 上方向 (Up)。

  2. 视图变换的最终目的是什么？

    将相机变换到标准位置（原点，看向-Z，+Y朝上），从而简化后续计算。

  3. 视图矩阵 $`M_{view}`$ 是由哪两种基本变换组合而成的？

    旋转 (Rotation) 和平移 (Translation)。

课堂总结

  • 明确了视图变换在渲染流水线中的位置和作用
  • 学会使用 lookAt 方法的三个向量来精确描述一个相机
  • 深入理解视图变换的本质：变换世界，而非相机。
  • 掌握了从相机三要素推导视图矩阵的完整过程。