计算机图形学

第二部分：基础变换

本部分内容：

• 旋转
• 缩放
• 平移

课程目标

• 解释 2D平移、旋转和缩放变换的几何意义
• 推导 并 写出 2D旋转和缩放的2x2矩阵
• 阐明 平移变换的特殊性，以及为何需要统一的表示方法
• 解释 齐次坐标的定义及其在图形学中的核心作用
• 使用 3x3的齐次矩阵来统一表示2D变换

变换的概念

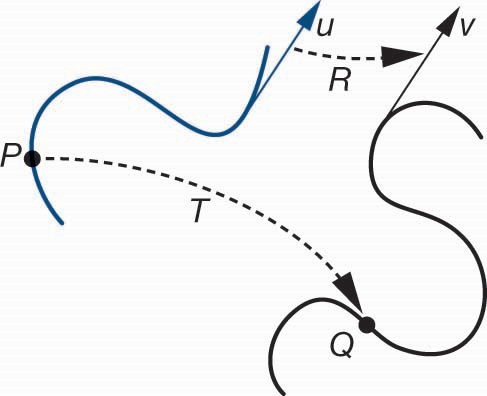
变换，指的是建立点与点或向量与向量之间的映射，如下图中所示，有映射关系$v=T(u)$，$Q=T(P)$

仿射变换

仿射变换，能够维持物体的线性属性，其中包含了物理上的重要的变换，如

• 刚性变换(Rigid-body transformation)：包括旋转(Rotation)、平移(Translation)
• 非刚性变换(Non-rigid transformation)：缩放(Scaling)、错切(Shear)

在计算机图形学中，仿射变换是非常重要的，仿射变换能保持拓扑结构不变，即点、线、面之间的相对关系保持不变

仿射变换流水线实现

旋转

考虑由上述四点构成的正四边形，若要实现按角速度$\theta$绕原点逆时针旋转的动画效果

即求点$P(x,y)$旋转$\theta$度后的新坐标$P'(x',y')$

推导过程

核心工具是，三角函数

1. 首先，用极坐标表示点 $P(x, y)$。设OP长度为 $r$，初始角度为 $\alpha$
2. 则有 \[ \begin{cases} x=r\cos{\alpha}\\ y=r\sin{\alpha} \end{cases} \]
3. 绕原点逆时针旋转$\theta$角度后，新点$P'$的角度变为$(\alpha + \theta)$，半径 $r$ 不变
4. 因此有： \[ \begin{cases} x'=r\cos{(\alpha + \theta)}\\ y'=r\sin{(\alpha + \theta)} \end{cases} \]
5. 接下来，我们需要展开这两个和角公式...

推导过程续

6. 根据和角公式，有： \[ \begin{cases} \cos{(\alpha + \theta)}=\cos{\alpha}\cos{\theta}-\sin{\alpha}\sin{\theta}\\ \sin{(\alpha + \theta)}=\sin{\alpha}\cos{\theta}+\cos{\alpha}\sin{\theta} \end{cases} \]
7. 将其代入$x',y'$的表达式，得到： \[ \begin{cases} x'=r\cos{(\alpha + \theta)}=r\cos{\alpha}\cos{\theta}-r\sin{\alpha}\sin{\theta}\\ y'=r\sin{(\alpha + \theta)}=r\sin{\alpha}\cos{\theta}+r\cos{\alpha}\sin{\theta} \end{cases} \]
8. 回忆一下，$x=r\cos{\alpha}$，$y=r\sin{\alpha}$，将其代入上式，得到： \[ \begin{cases} x'=x\cos{\theta}-y\sin{\theta}\\ y'=x\sin{\theta}+y\cos{\theta} \end{cases} \]

推导过程续(2)

9. 将上式改写成矩阵形式： \[ \begin{bmatrix} x'\\y' \end{bmatrix}= \begin{bmatrix} \cos{\theta} & -\sin{\theta}\\ \sin{\theta} & \cos{\theta} \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} \]

该矩阵即为在二维平面点$P$绕原点逆时针旋转$\theta$度的旋转矩阵

旋转矩阵可视化

缩放

如何让一个点 $P(x, y)$，以原点为中心，在水平方向上放大 $S_x$ 倍，在垂直方向上放大 $S_y$ 倍，得到新的坐标 $P'(x', y')$？

推导过程

缩放的逻辑非常直接：

1. 新的x坐标 $x'$ 是旧的x坐标 $x$ 乘以水平缩放因子 $S_x$
2. $x' = S_x x$
3. 同理，新的y坐标 $y'$ 是旧的y坐标 $y$ 乘以垂直缩放因子 $S_y$
4. $y' = S_y y$
5. 这两个简单的方程就是缩放变换的核心！

推导过程续

6. 将上面两个方程合并： \[ \begin{cases} x' = S_x x\\ y' = S_y y \end{cases} \]
7. 为了统一成矩阵形式，我们可以将它们看作是 $x$ 和 $y$ 的线性组合，其中一些系数为0 \[ \begin{cases} x' = S_x x + {\color{gray}0 \cdot y}\\ y' = {\color{gray}0 \cdot x} + S_y y \end{cases} \]
8. 将上式改写成矩阵形式： \[ \begin{bmatrix} x'\\y' \end{bmatrix}= \begin{bmatrix} S_x & 0\\ 0 & S_y \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} \]

该矩阵即为在二维平面点$P$以原点为中心按比例$S_x$和$S_y$缩放的缩放矩阵

缩放矩阵可视化

平移

如何将一个点$P(x,y)$平移一段固定的距离$(t_x,t_y)$，到达新的位置$P'(x',y')$?

用数学表达

从数学上看，平移是最简单的操作，就是坐标的加法：

问题来了：能像旋转和缩放一样，用一个$2\times 2$的矩阵来表示这个加法操作吗？

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \]

$2\times 2$矩阵的局限性

如果能构建矩阵，则有

\[ \begin{cases} x'=ax+by\\ y'=cx+dy \end{cases} \]

会发现，无论如何选择$a,b,c,d$，都无法制造出一个独立的加法项$t_x$或$t_y$

使用齐次坐标和齐次矩阵

为了表示平移，需要扩展表示的维度，使用齐次坐标表示点，并使用齐次矩阵表示平移

$$ P(x,y)\Rightarrow P_h(x,y,{\color{red}1} )$$

计算$3\times 3$矩阵

目标是，找到一个$3\times 3$的矩阵，满足

\[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} ? & ? & ? \\ ? & ? & ? \\ ? & ? & ? \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

计算后满足

\[ \begin{cases} x' = x + t_x \\ y' = y + t_y \\ 1 = 1 \end{cases} \]

计算$3\times 3$矩阵

根据矩阵乘法计算规则展开，可以得到

• \[ x'=?x+?y+?1={\color{red}1}\cdot x + {\color{red}0}\cdot y + {\color{red}t_x}\cdot 1 \]
• \[ y'=?x+?y+?1={\color{red}0}\cdot x + {\color{red}1}\cdot y + {\color{red}t_y}\cdot 1 \]
• \[ 1=?x+?y+?1={\color{red}0}\cdot x + {\color{red}0}\cdot y + {\color{red}1}\cdot 1 \]

齐次平移矩阵

因此，齐次平移矩阵为

\[ M=\begin{bmatrix} 1 & 0 & {\color{red}t_x} \\ 0 & 1 & {\color{blue}t_y} \\ 0 & 0 & 1 \end{bmatrix} \]

\[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} =\begin{bmatrix} x+x_t\\ y+y_t\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & {\color{red}t_x} \\ 0 & 1 & {\color{blue}t_y} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

观察平移矩阵的结构，可以发现

• 平移矩阵的左上角为$2\times 2$的单位矩阵，保证坐标系的不变性
• 最后一列前两项$(t_x, t_y)$为平移的距离

平移矩阵可视化

三种变换矩阵

到目前为止的三种基本变换矩阵分别对应：

是否可以将旋转和缩放也“升级”到$3\times 3$矩阵呢？

缩放矩阵

将$2\times 2$的缩放矩阵变成$3\times 3$的齐次矩阵有：

\[ \begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} s_x & 0 & ? \\ 0 & s_y & ? \\ ? & ? & ? \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \]

将矩阵展开后求解，可得到：

\[ M=\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

旋转矩阵

将$2\times 2$的旋转矩阵变成$3\times 3$的齐次矩阵有：

\[ \begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta & ? \\ \sin \theta & \cos \theta & ? \\ ? & ? & ? \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \]

将矩阵展开后求解，可得到：

\[ M=\begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

齐次矩阵统一表示

现在我们有了三种基本变换的齐次矩阵表示：

变换可视化

三维空间的变换

三维空间中的变换与二维空间类似，只是多了z轴的变换。

平移

空间中，将一个点$P(x,y,z)$移动到新的点位置$P'(x',y',z')$，位移向量为$(t_x, t_y, t_z)$，即有

\[ \begin{cases} x' = x + t_x \\ y' = y + t_y \\ z' = z + t_z \end{cases} \]

三维空间的变换

平移对应的变换矩阵记为$T$，有$P'=TP$， 其中，$T$为

\[ T(t_x, t_y, t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

三维空间的变换

缩放

三维空间中，沿着三条轴的方向改变对象的大小，假设在三条轴方向上缩放系数分别为$s_x, s_y, s_z$，其表达式可写成

\[ \begin{cases} x' = s_x \cdot x \\ y' = s_y \cdot y \\ z' = s_z \cdot z \end{cases} \]

缩放对应的变换矩阵记为$S$，有$P'=SP$， 其中，$S$为

\[ S(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

三维空间的变换

反射可视作是特殊的缩放

\[ \begin{cases} s_x=1, s_y=1\\ s_x=-1, s_y=1\\ s_x=-1, s_y=-1\\ s_x=1, s_y=-1 \end{cases} \]

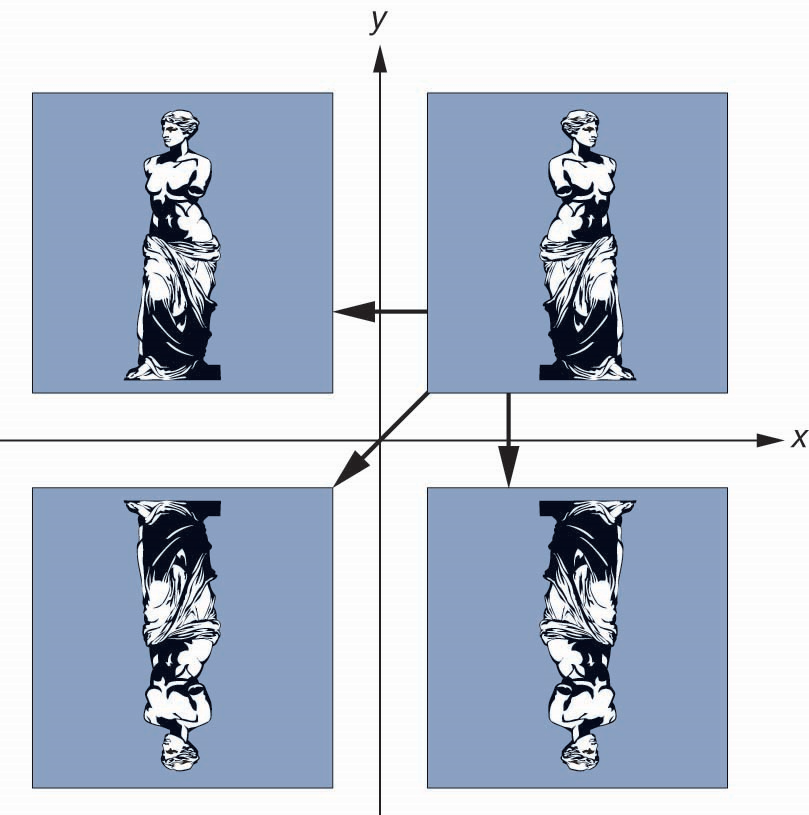
三维空间的变换

旋转

三维空间中，旋转定义为绕特定坐标轴的转动

绕$Z$轴旋转$\theta$角，保持点坐标的$Z$分量不变

三维空间的变换

点$(x,y,z)$绕$Z$轴逆时针(正向)旋转$\theta$角度，相当于是点在$XOY$平面绕原点旋转在三维空间的扩展，有

\[ \begin{cases} x' = x \cdot \cos \theta - y \cdot \sin \theta \\ y' = x \cdot \sin \theta + y \cdot \cos \theta \\ z' = z \end{cases} \]

对应的齐次旋转变换矩阵记为$R_{Z}(\theta)$，有$P'=R_{Z}(\theta)P$， 其中，$R_{Z}(\theta)$为

\[ R_{Z}(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

三维空间的变换

相应的，绕$X$轴和$Y$轴正向分别旋转$\theta$角度，保持相应的分量值不变

三维空间的变换

利用与$Z$轴相同的方式，可推导得到绕$X$轴和$Y$轴旋转的齐次坐标矩阵表示分别为：

绕任意点的旋转

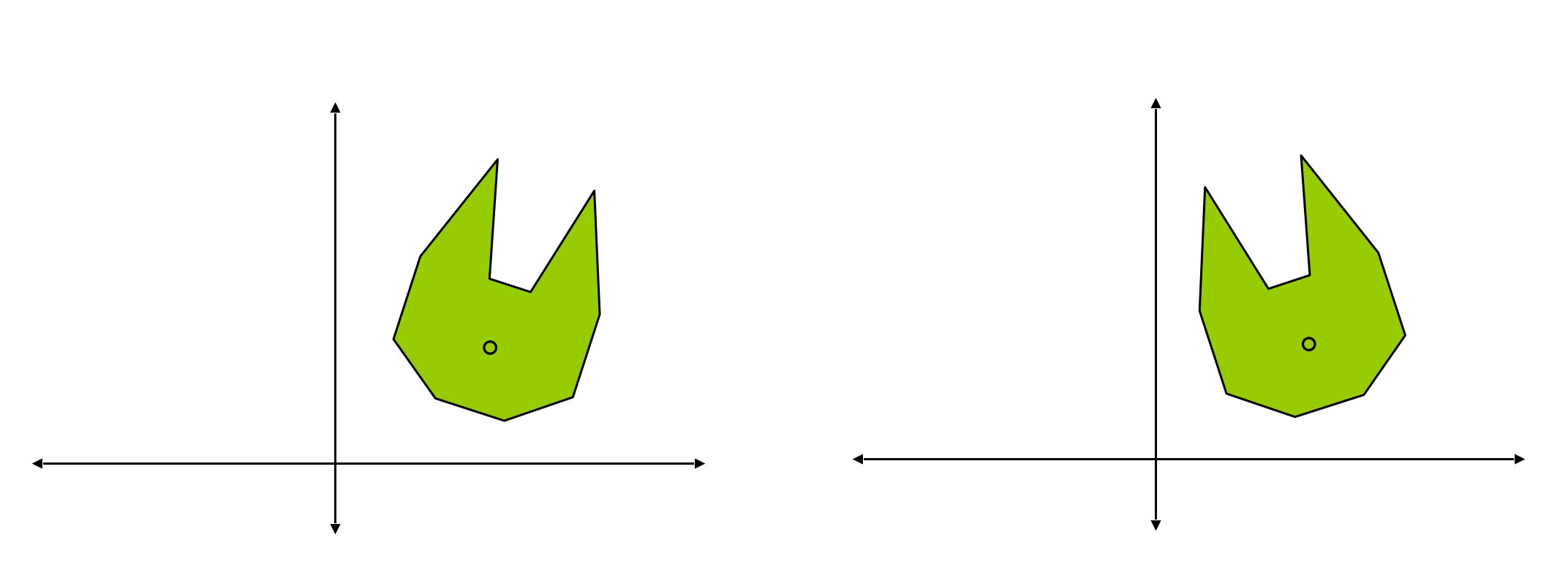
思考，如何实现绕任意点的旋转？