计算机图形学

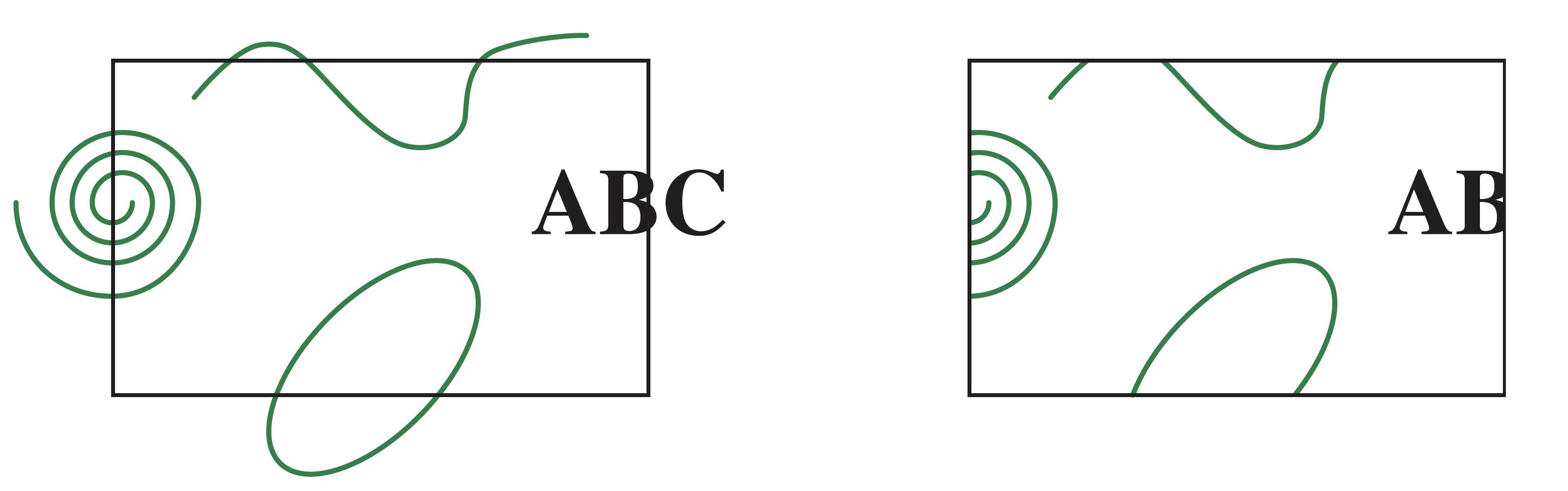
裁剪

Cohen-Sutherland算法(1)

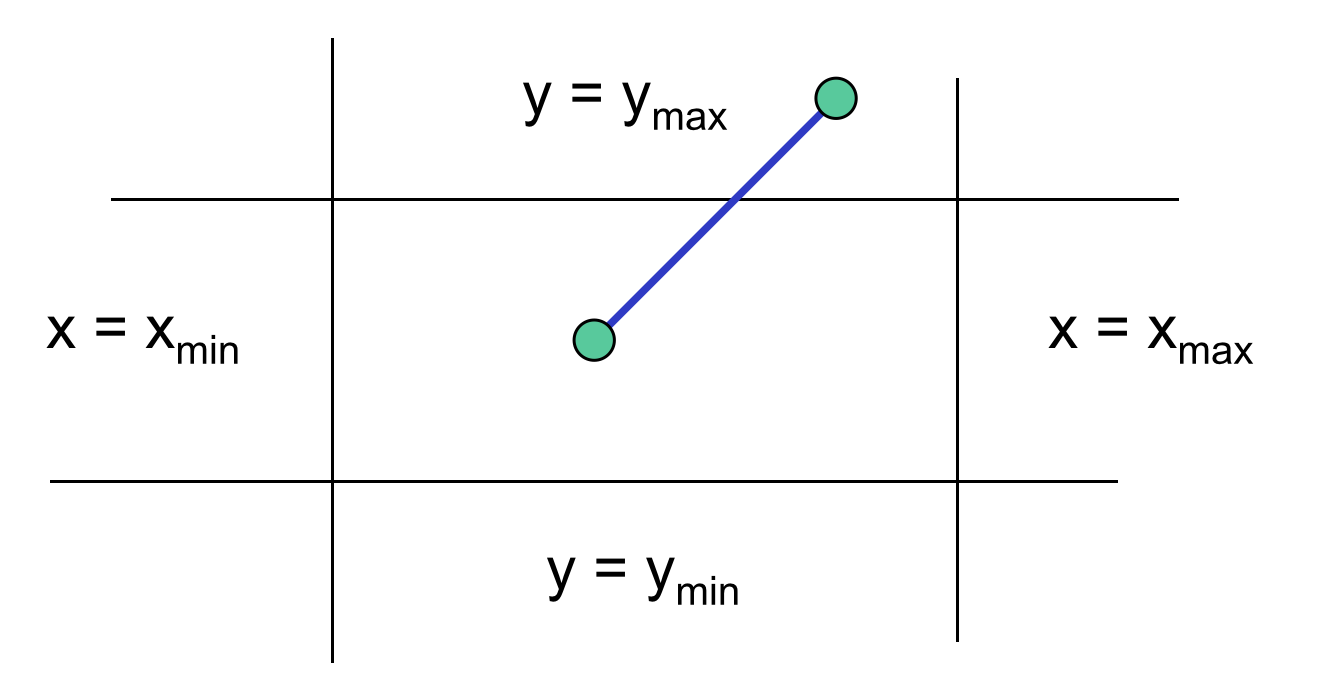
Cohen-Sutherland算法的主要思路是尽可能不通过计算交点去除各种可能的情况。首先需要用四条线确定裁剪窗口的大小

裁剪

Cohen-Sutherland算法(2)

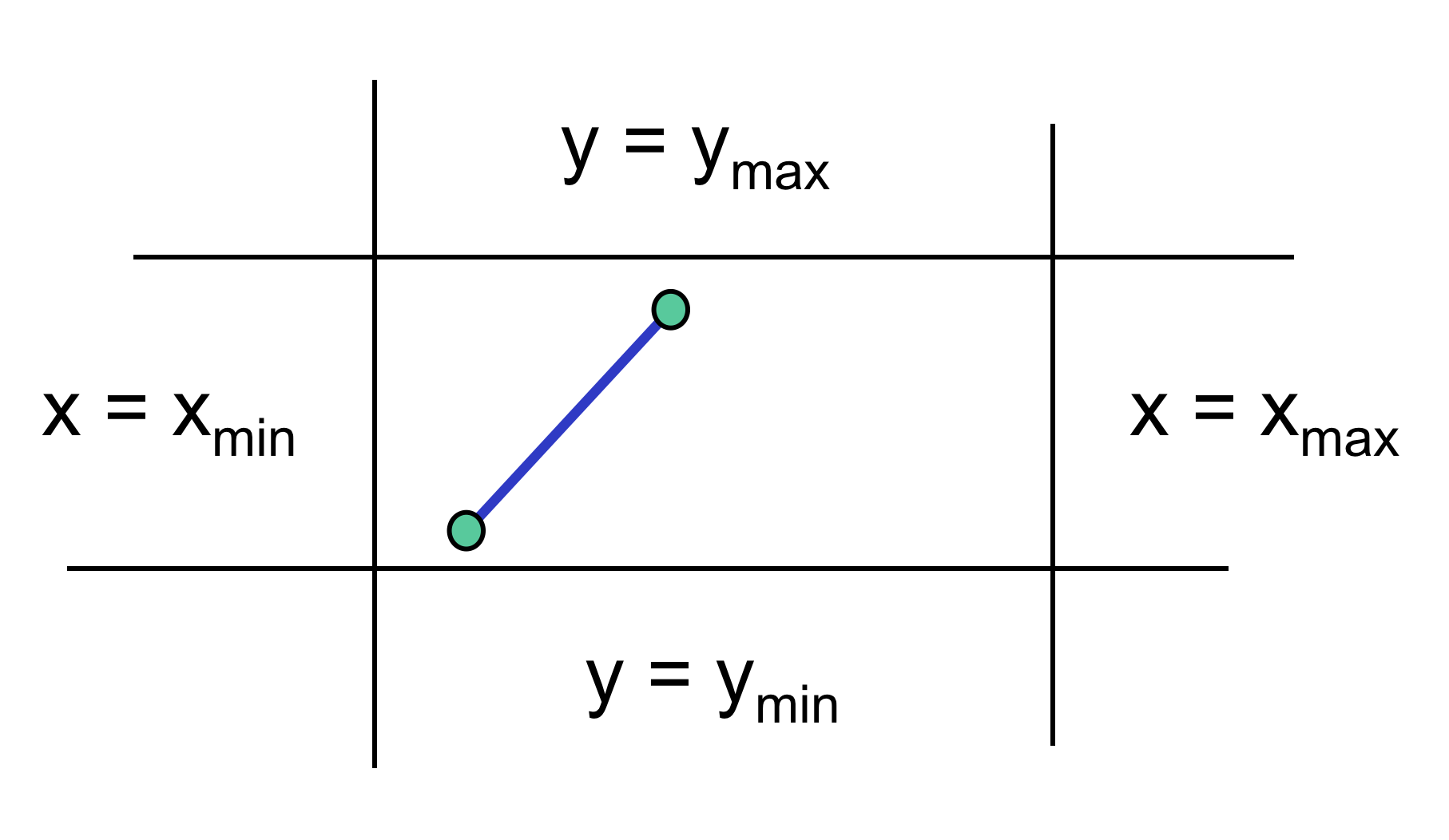
对每条线的两个端点，定义相应的区域编码

情况1. 线段的两个顶点都位于裁剪窗口内，则接受整条线段

裁剪

Cohen-Sutherland算法(3)

情况2. 线段两个顶点都位于裁剪窗口外，且两个顶点都位于四条边界线的同侧，则拒绝整条线段

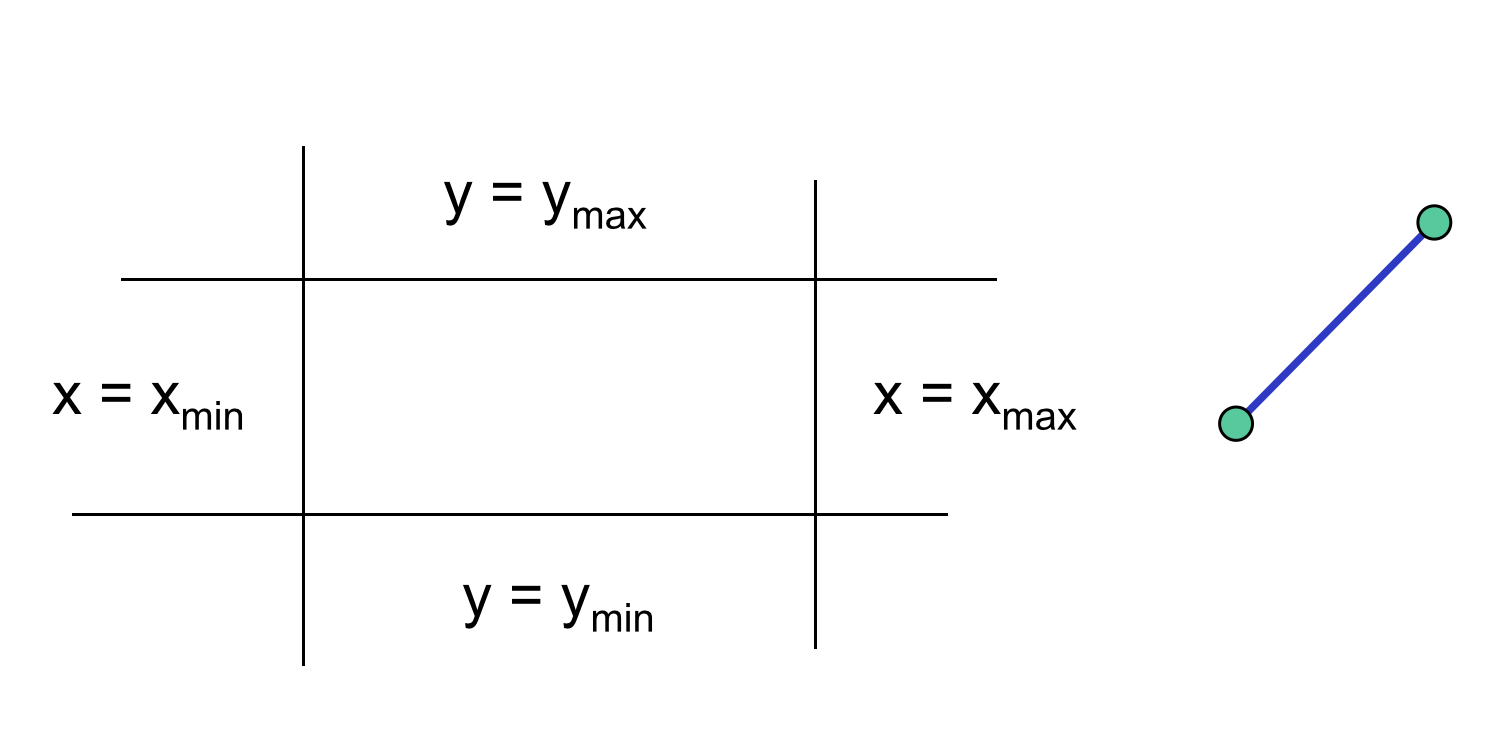
裁剪

Cohen-Sutherland算法(4)

情况3. 线段的两个顶点，一个位于裁剪窗口内，一个位于裁剪窗口外，需要处理至少一个交点

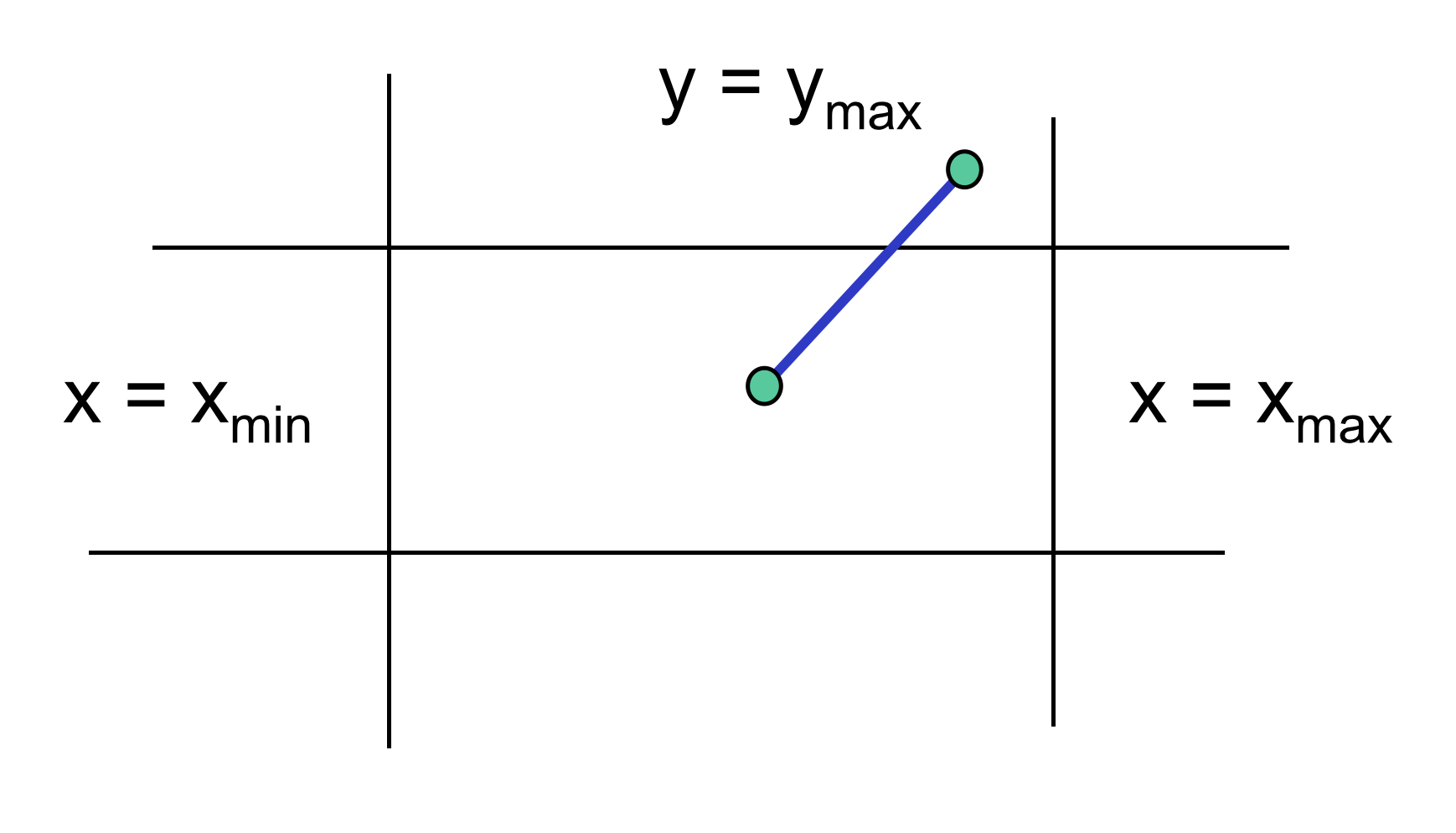
裁剪

Cohen-Sutherland算法(5)

情况4. 线段的两个顶点都位于裁剪窗口外，但线段都有部分位于裁剪窗口内，需要处理至少一个交点

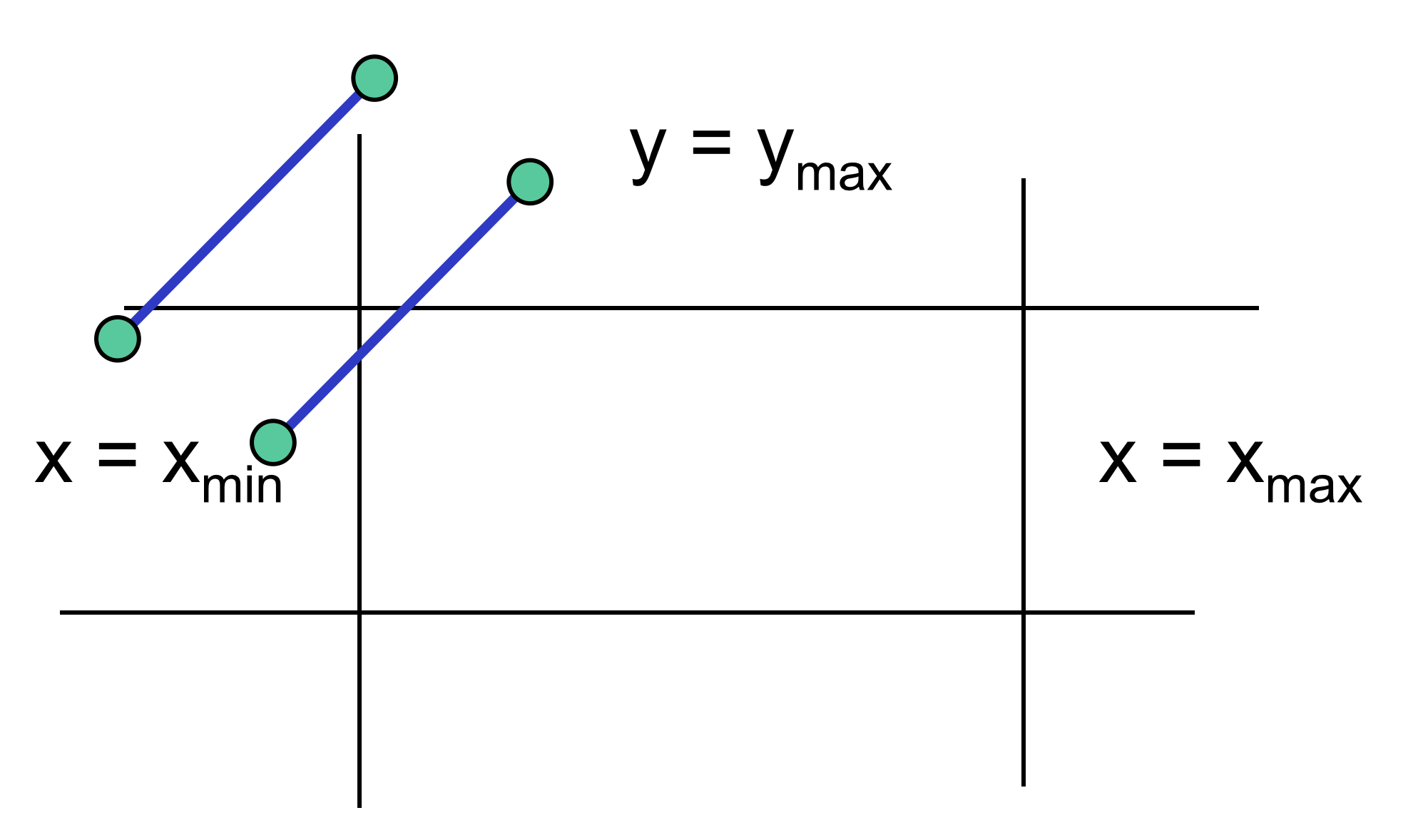
裁剪

定义区域编码

对线段的每个顶点，定义区域码，区域码由四位数字构成，表示成$b_0b_1b_2b_3$，区域码将平面分割成9个部分，计算区域编码需要进行最多4次减法计算，有

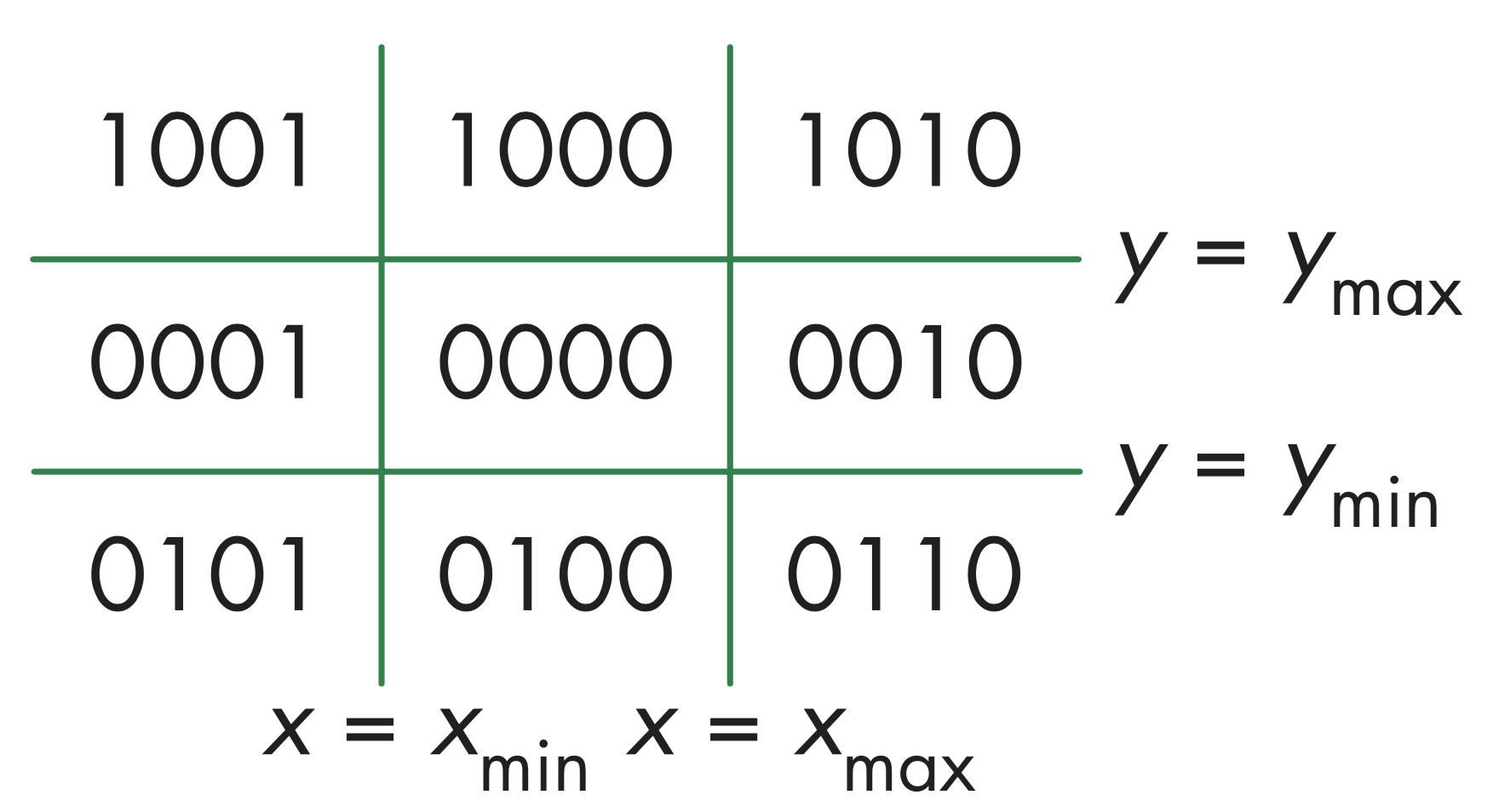
裁剪

区域码示例

考虑如下图中5种情形:

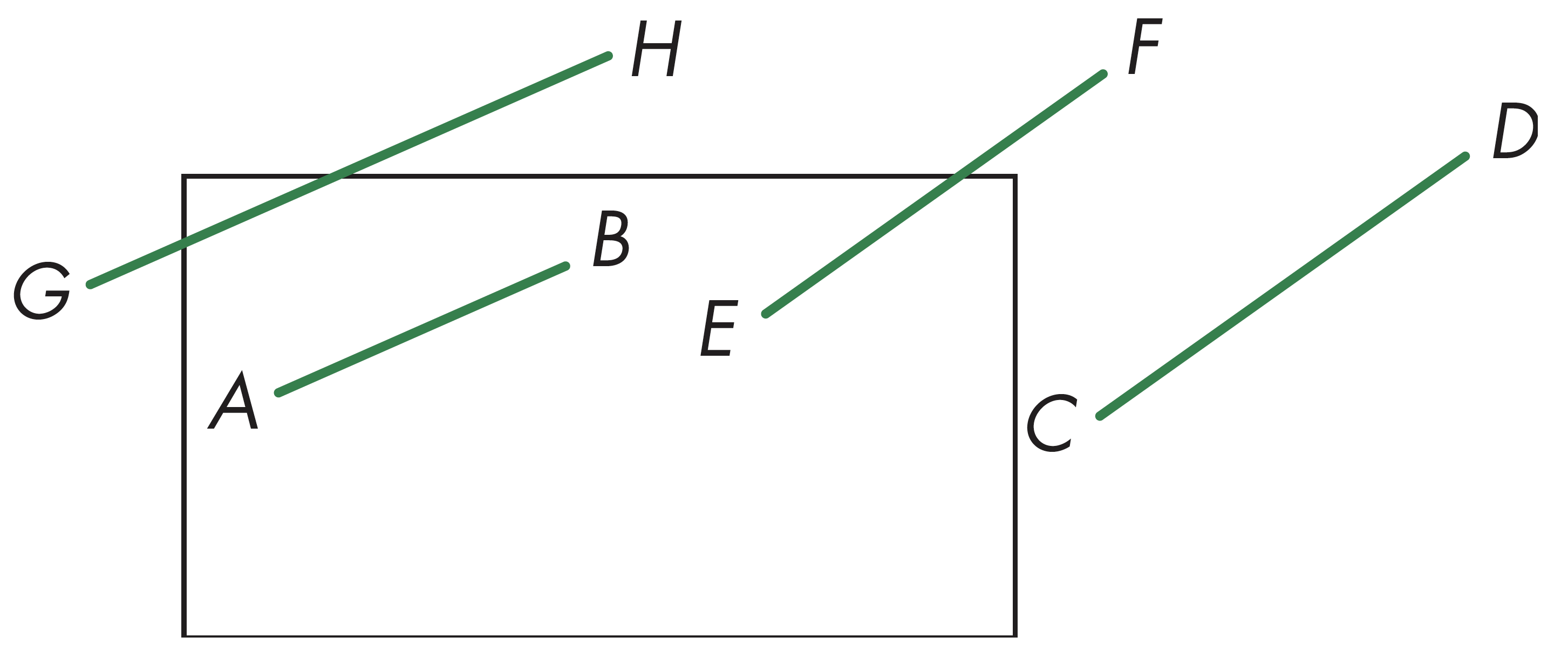
对于直线AB: 有$outcode(A)=outcode(B)=0$，接受直线AB

裁剪

区域码示例

对于直线CD: 有$outcode(C)=0$, $outcode(D)\neq 0$，首先计算交点，outCode(D)中1的位置确定了CD和哪条边相交，若从A点开始连接某点的直线对应的outcode中有两个1，则需要处理两个直线交点

裁剪

区域码示例

对于直线EF: 将$outcode(E)$和$outcode(F)$按位与后结果非0，表明两个outcode有至少一个相同的位置上均为1，即表明该线段位于相应的裁剪窗口的外面，因此舍弃

裁剪

区域码示例

对于直线GH和IJ: 其端点的$outcode$值相同，均非0，但按位与后结果均为0，可将线段缩短后使之与窗口的一条边相交，计算相交点的区域码，然后再重复执行

裁剪

Cohen-Sutherlandd算法效率

大多应用中，裁剪窗口比整体对象数据要小，大部分直线在都会在裁剪窗口一条或多条边外，可根据其结果进行相应裁剪。但是，如果需要通过两个或以上步骤对直线进行缩减，算法需要不断重复执行时，计算效率会受到影响

裁剪

三维空间Cohen-Sutherland算法

在三维空间应用Cohen-Sutherland算法，需用6位区域编码，裁剪区域为一个由平面构成的空间区域

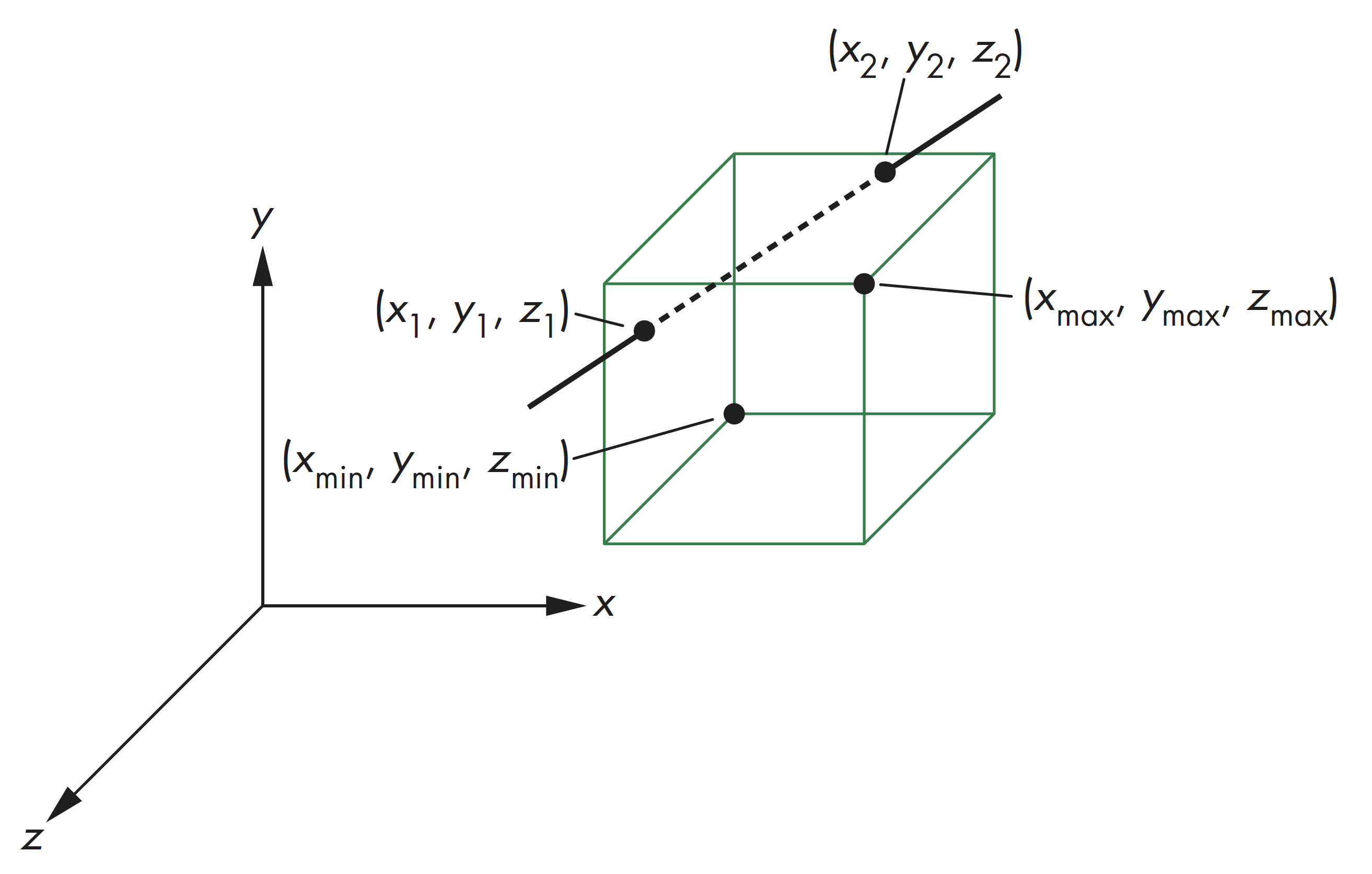
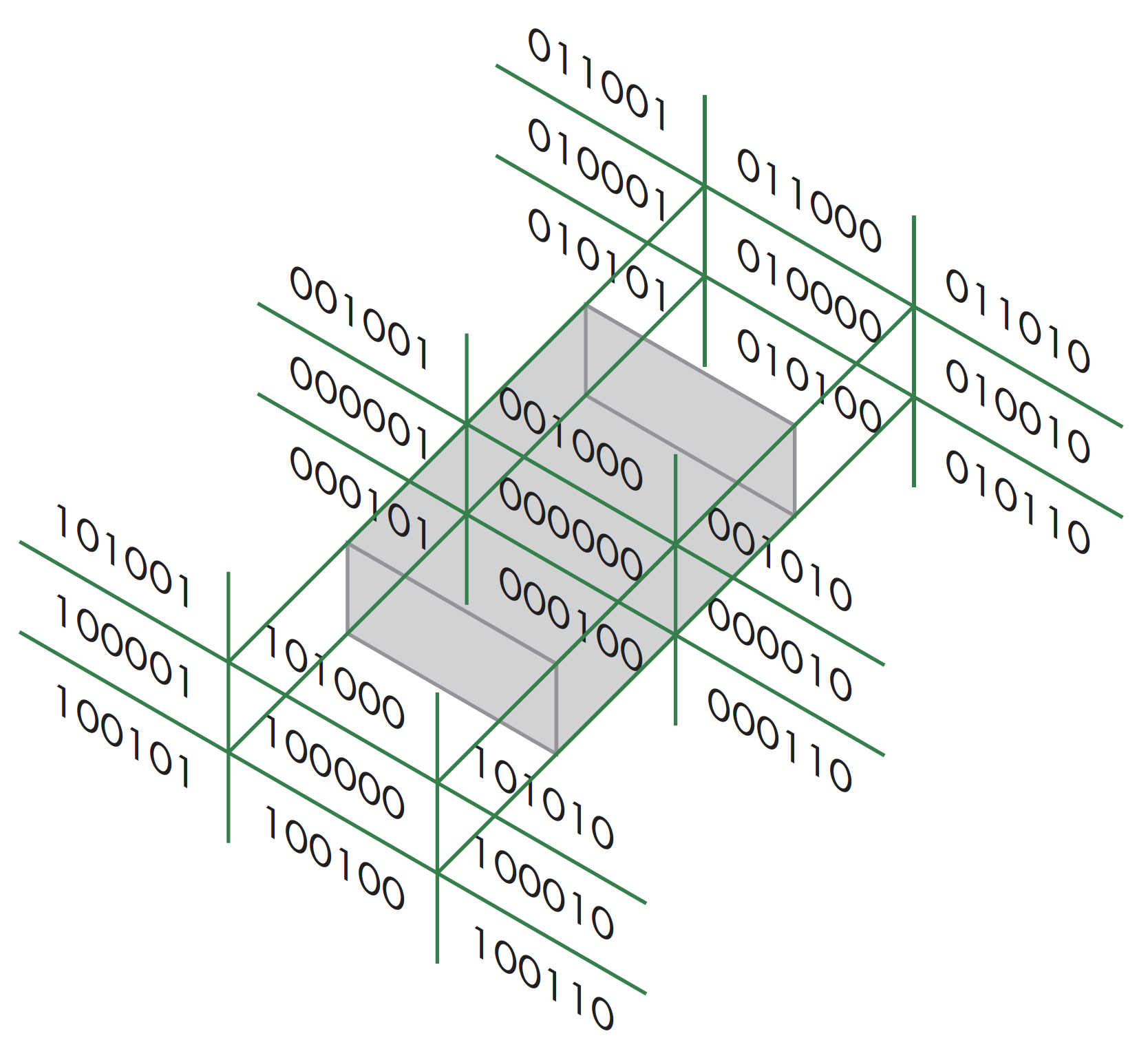
裁剪

裁剪和正则化

三维空间的一般化裁剪需要计算线段与任意平面之间的交战，比如下面两图分别示意了在正交和斜投影视图下的情况

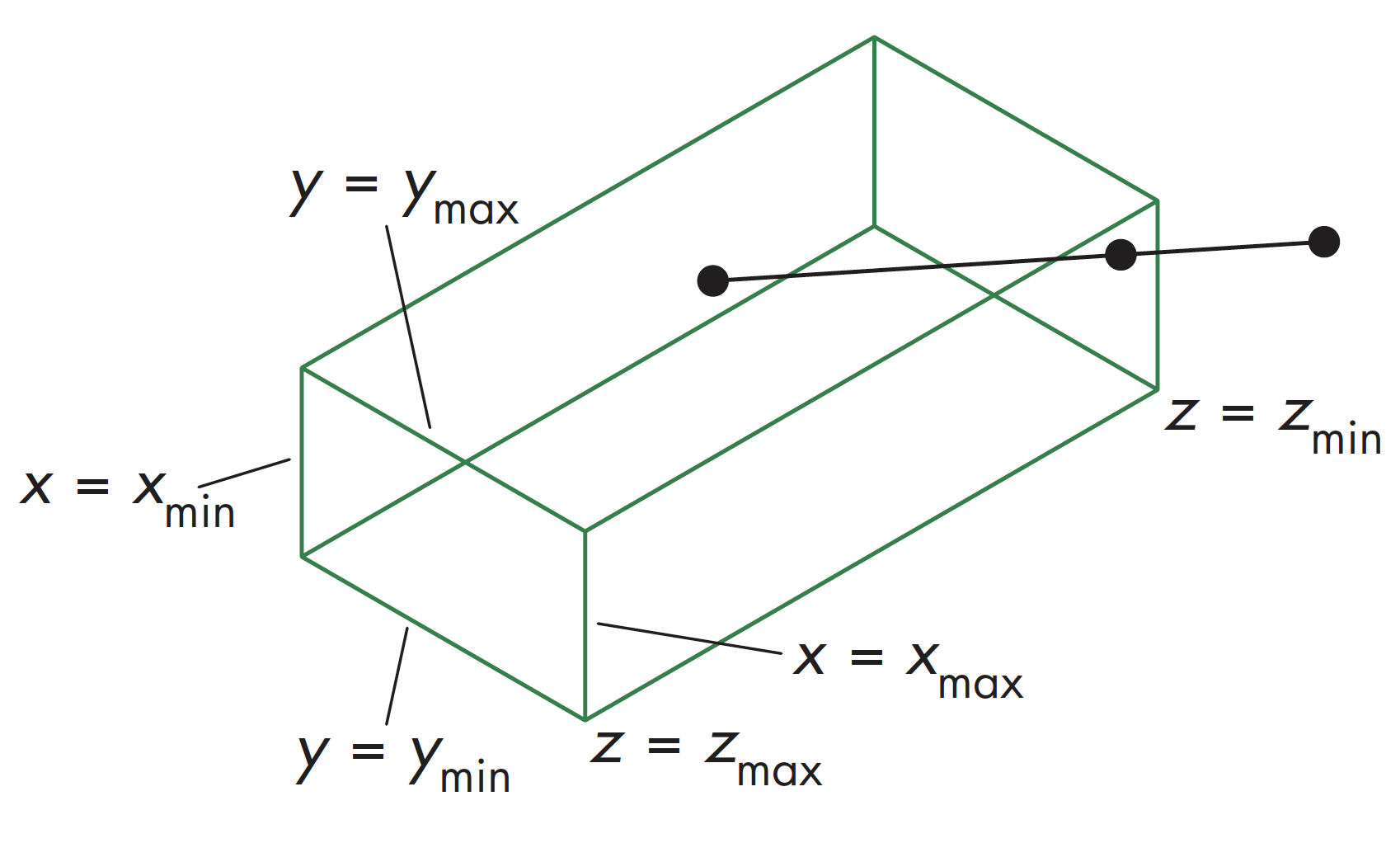
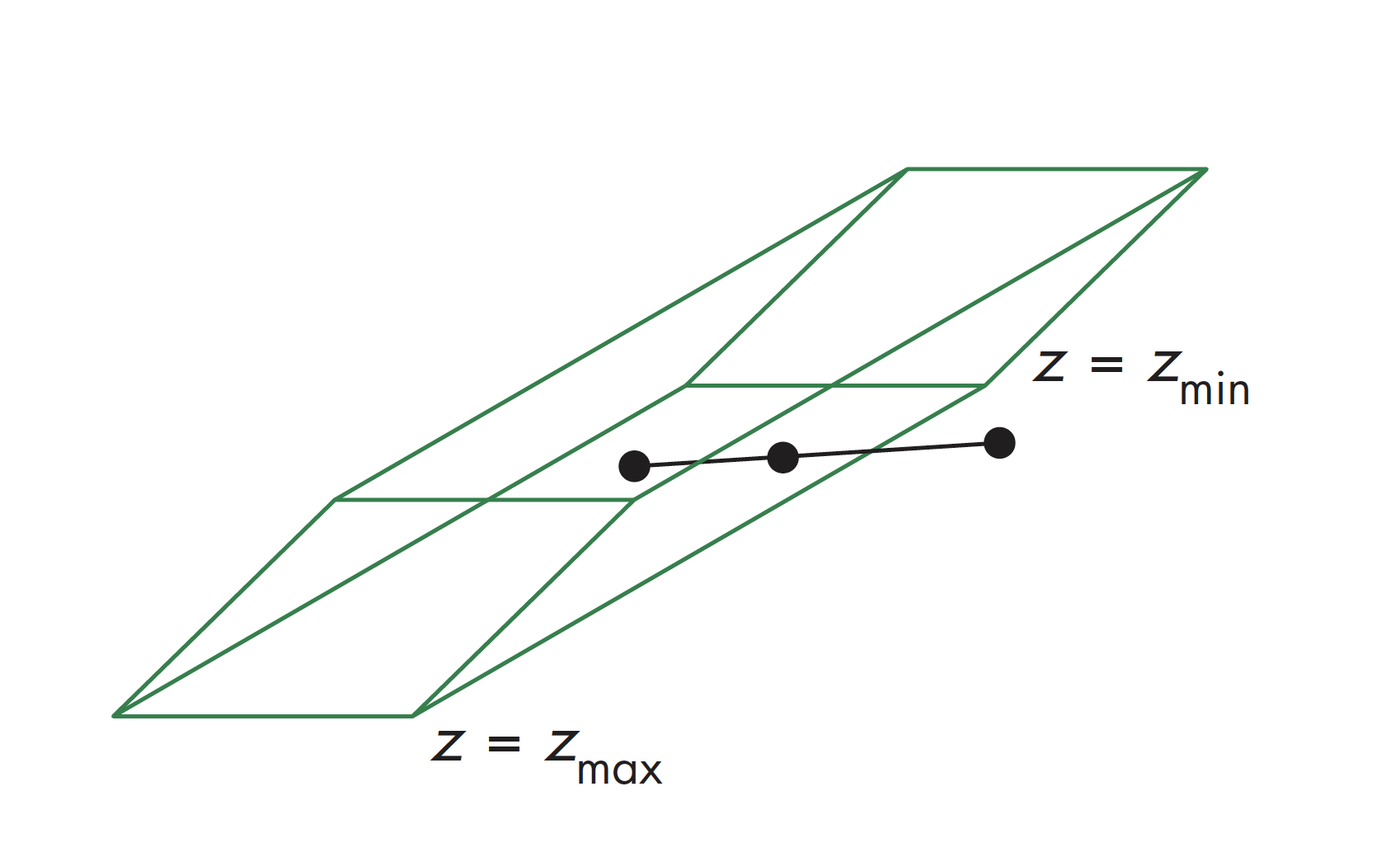
裁剪

正则化

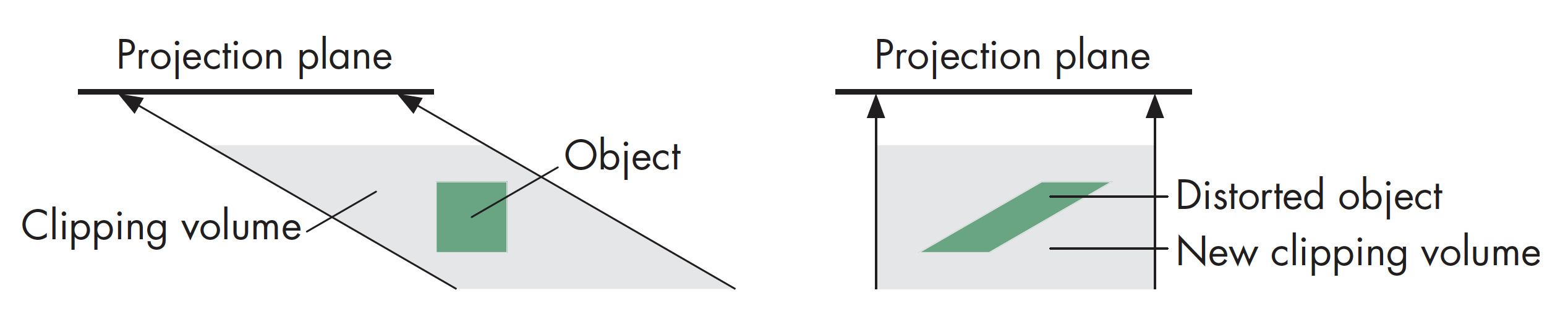
正则化可看作是投影成像的一部分，正则化后，可以相对右平行六面体的各面计算裁剪，且一般的相交计算只需要计算两个浮点数之间的差值即可/p>

裁剪

线和平面相交

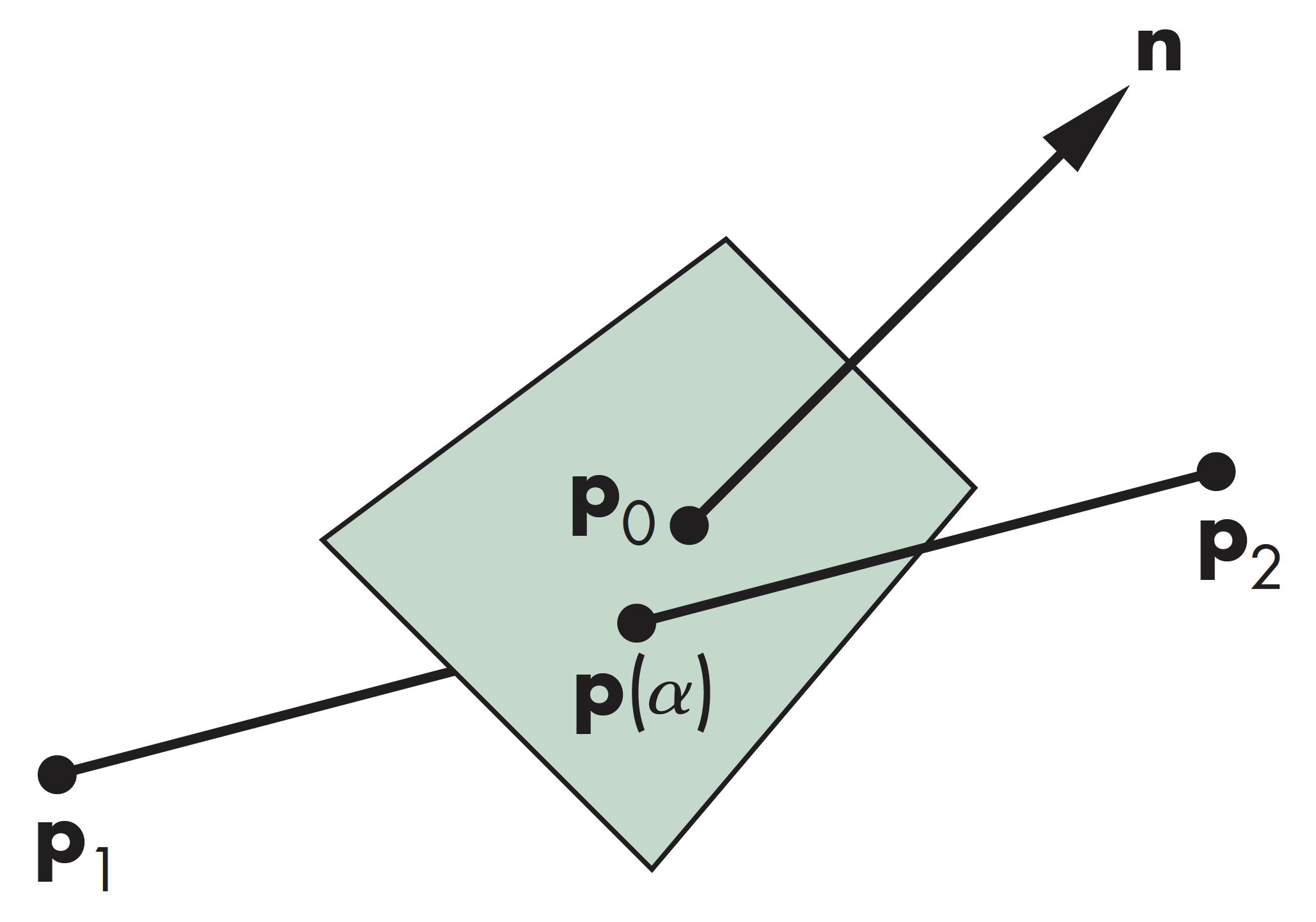
$$ \alpha=\frac{n\cdot(p_0-p_1)}{n\cdot(p_2-p_1)} $$

裁剪

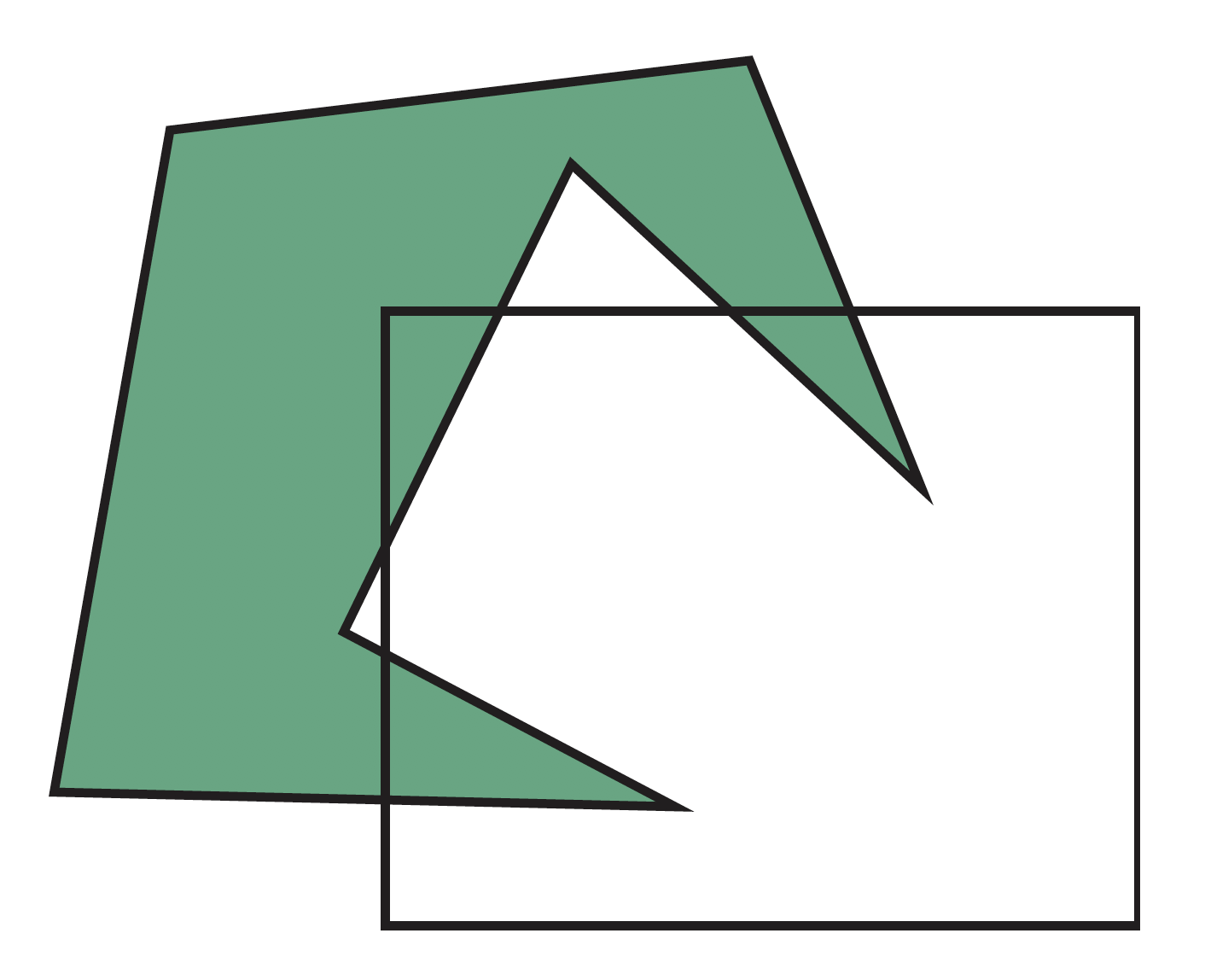
多边形裁剪

多边形裁剪比线段裁剪要复杂，对一条线段进行裁剪会产生最多一条线段，但对一个多边形裁剪会生成多个多边形，但是对凸多边形进行裁剪只会产生最多一个多边形

裁剪

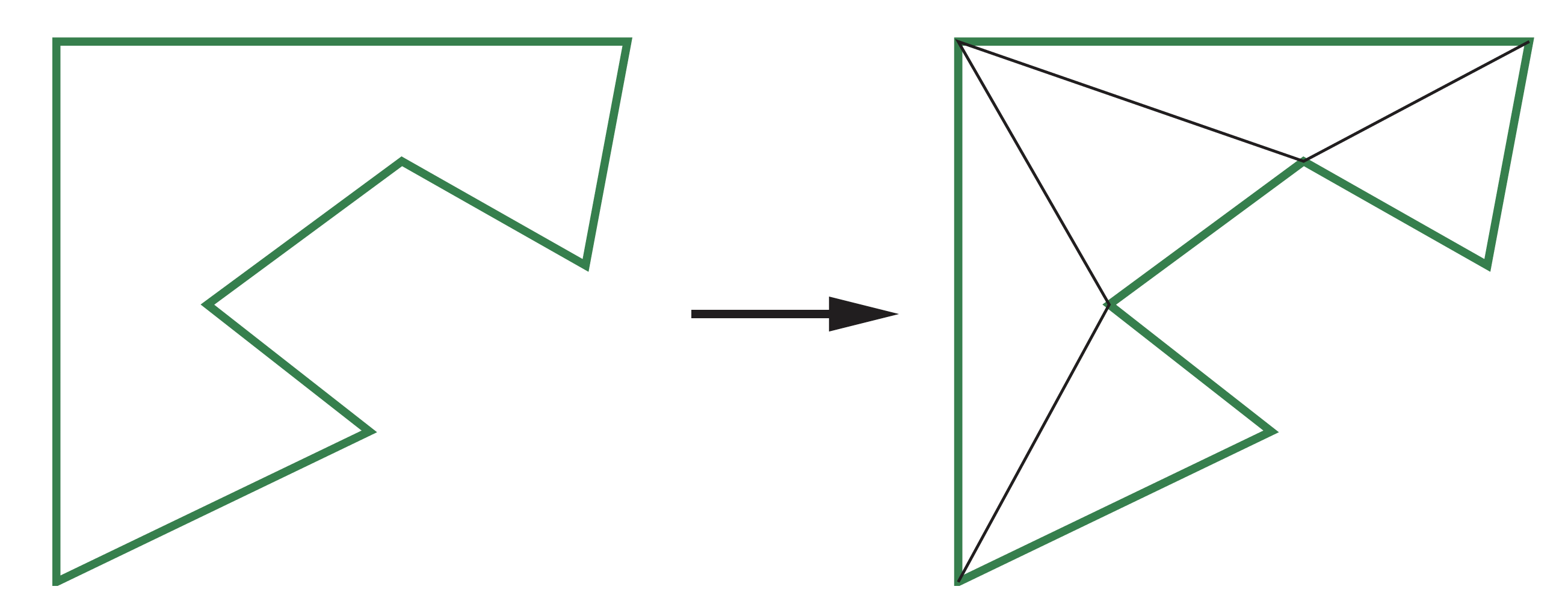
镶嵌和凸包性

对于非凸多边形，可以将其剖分为一组三角形

裁剪

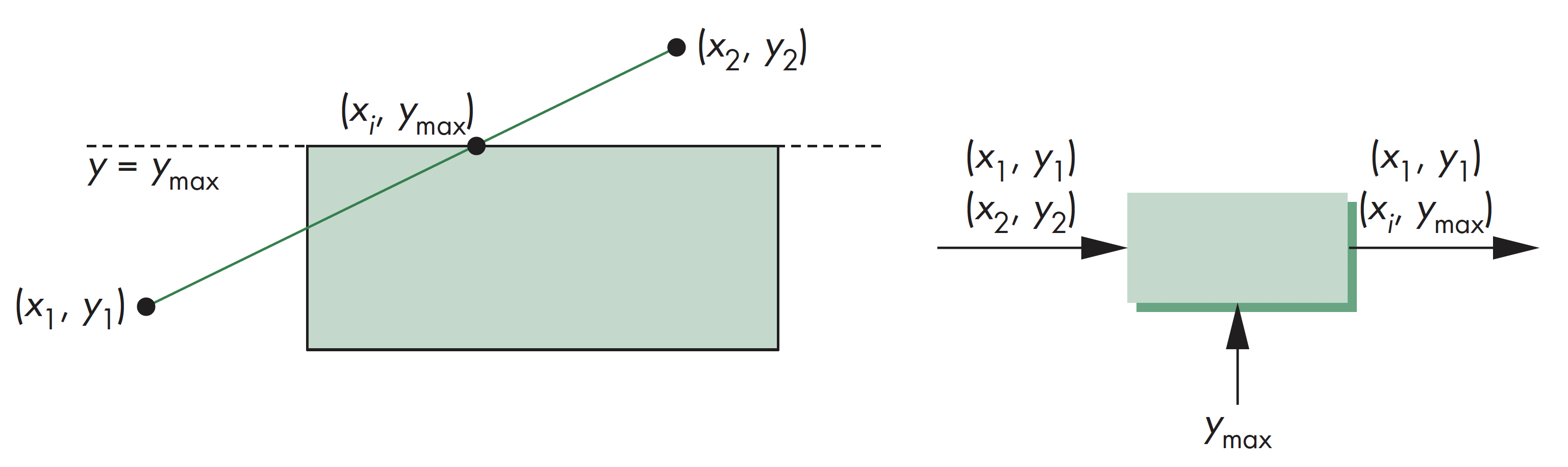
黑盒裁剪

线段裁剪可以视作黑盒操作，输入为两个顶点，输出要么无顶点，要么为经过裁剪后的线段顶点

裁剪

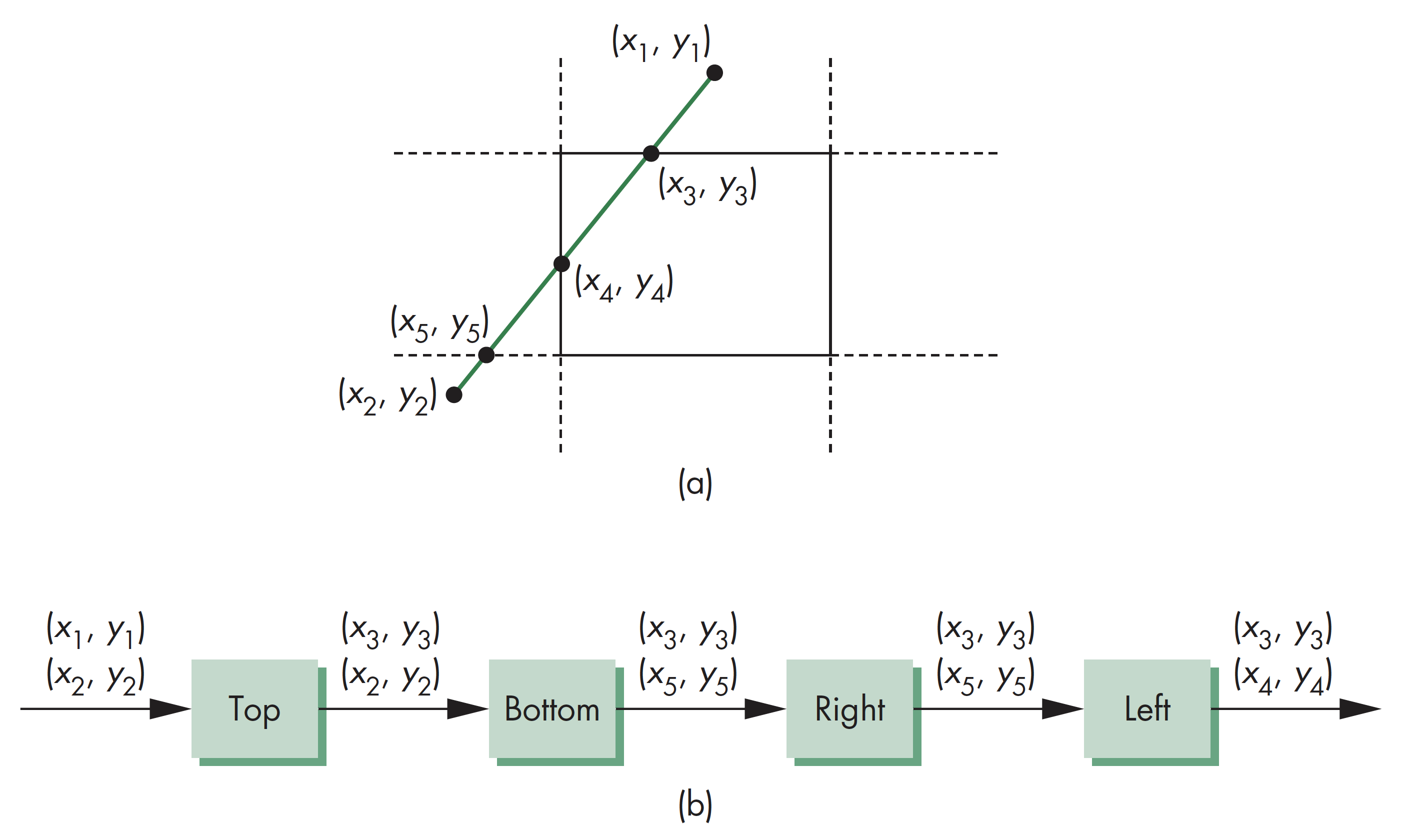
裁剪流水线

相对裁剪窗口各边或裁剪空间各面的裁剪计算都是独立的，因此可以在流水线上分别独立计算裁剪结果

裁剪

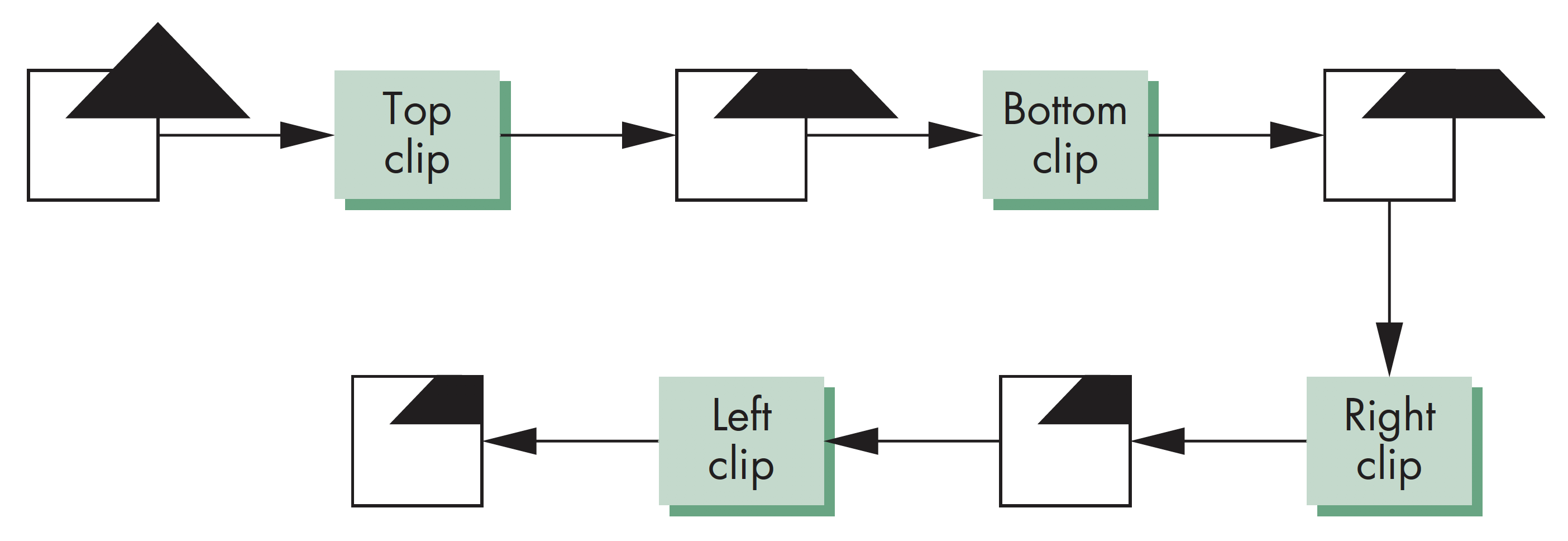
裁剪示例

示例为二维平面上的多边形裁剪，如果要进行三维空间裁剪，只需加上前面和后面，该方法应用于SGI几何引擎中，只有少量的延迟

裁剪

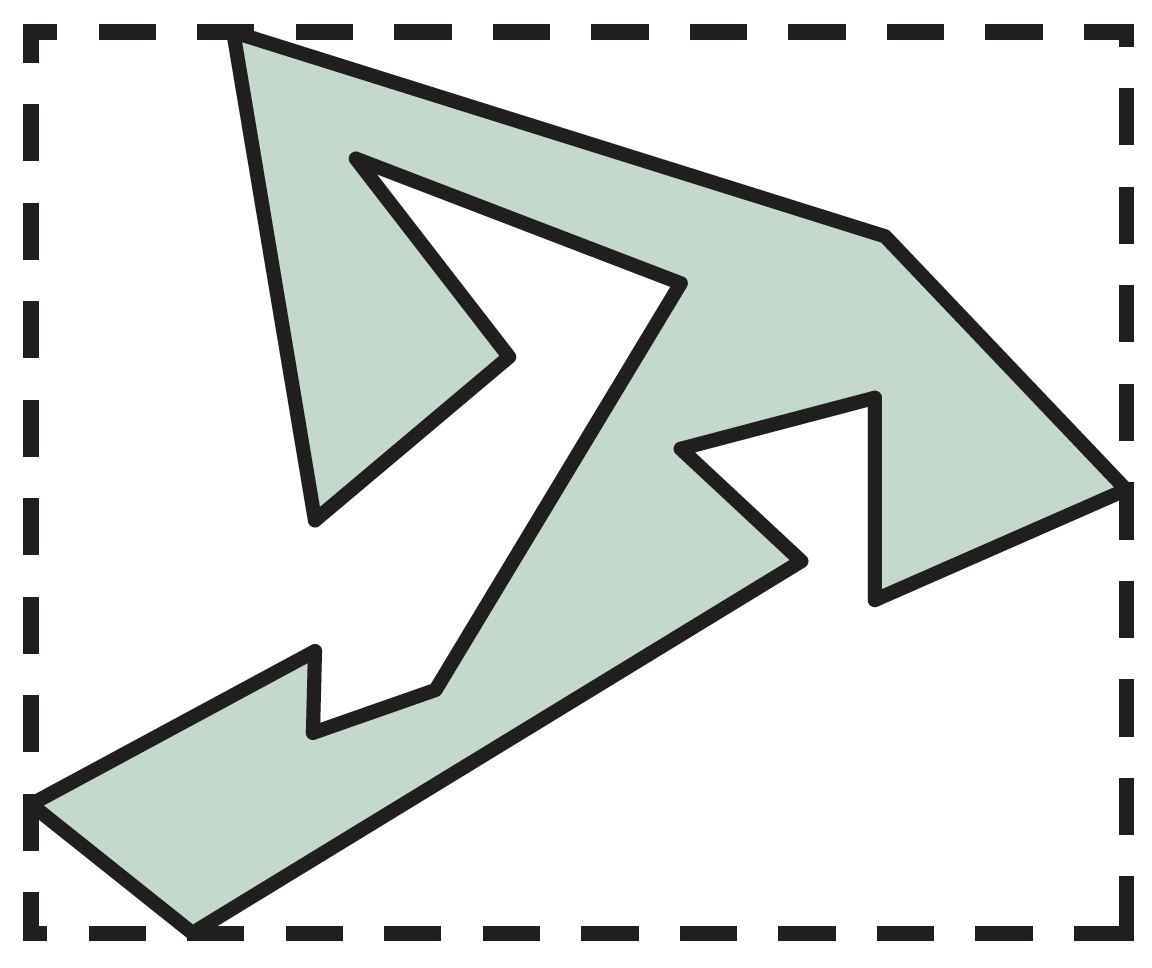
包围盒

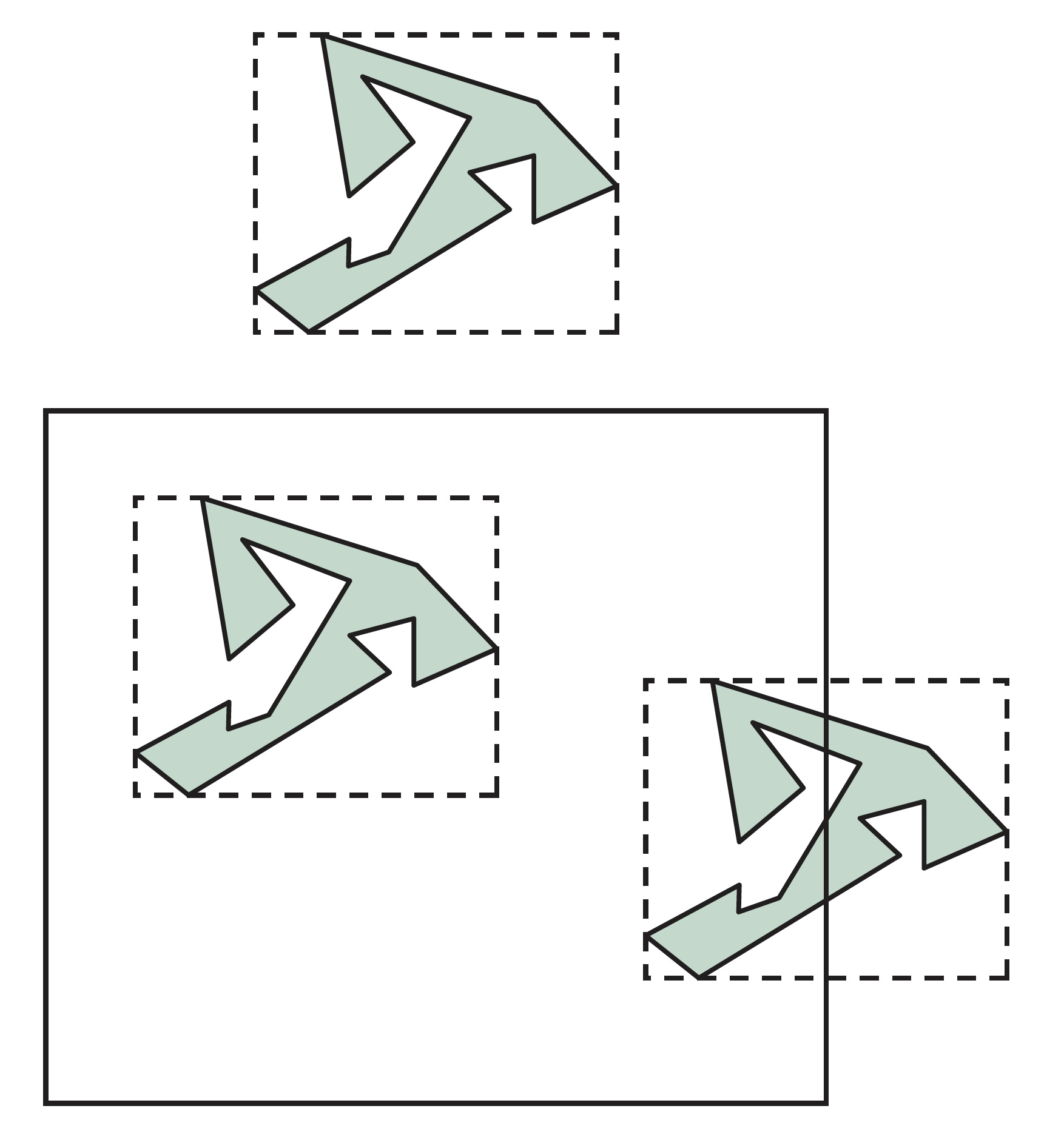
对复杂多边形进行裁剪，可先利用与坐标轴平行的包围盒，即用最小的与坐标轴平行的矩形区域包围住目标对象，其计算很简单，只需计算x和y轴方向的最大最小值即可

一般也可直接根据包围盒的裁剪结果决定是否接受或裁剪