计算机图形学

投影

投影和归一化

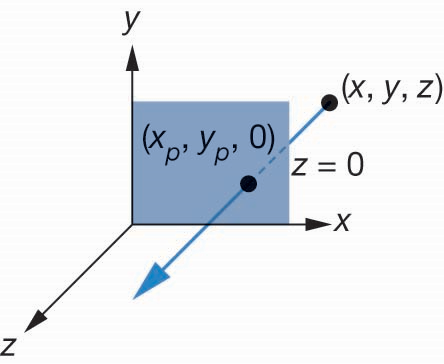
• 相机默认投影为正投影
• 对位于成像空间中的点，有 $$ \begin{cases} x_p=x\\ y_p=y\\ z=0 \end{cases} $$
• 大部分图形系统采用成像归一化，即
• 将所有其它的投影成像通过变换将其变换到默认成像空间
• 可以对所有的成像应用同样的管线处理

投影

齐次坐标矩阵

投影

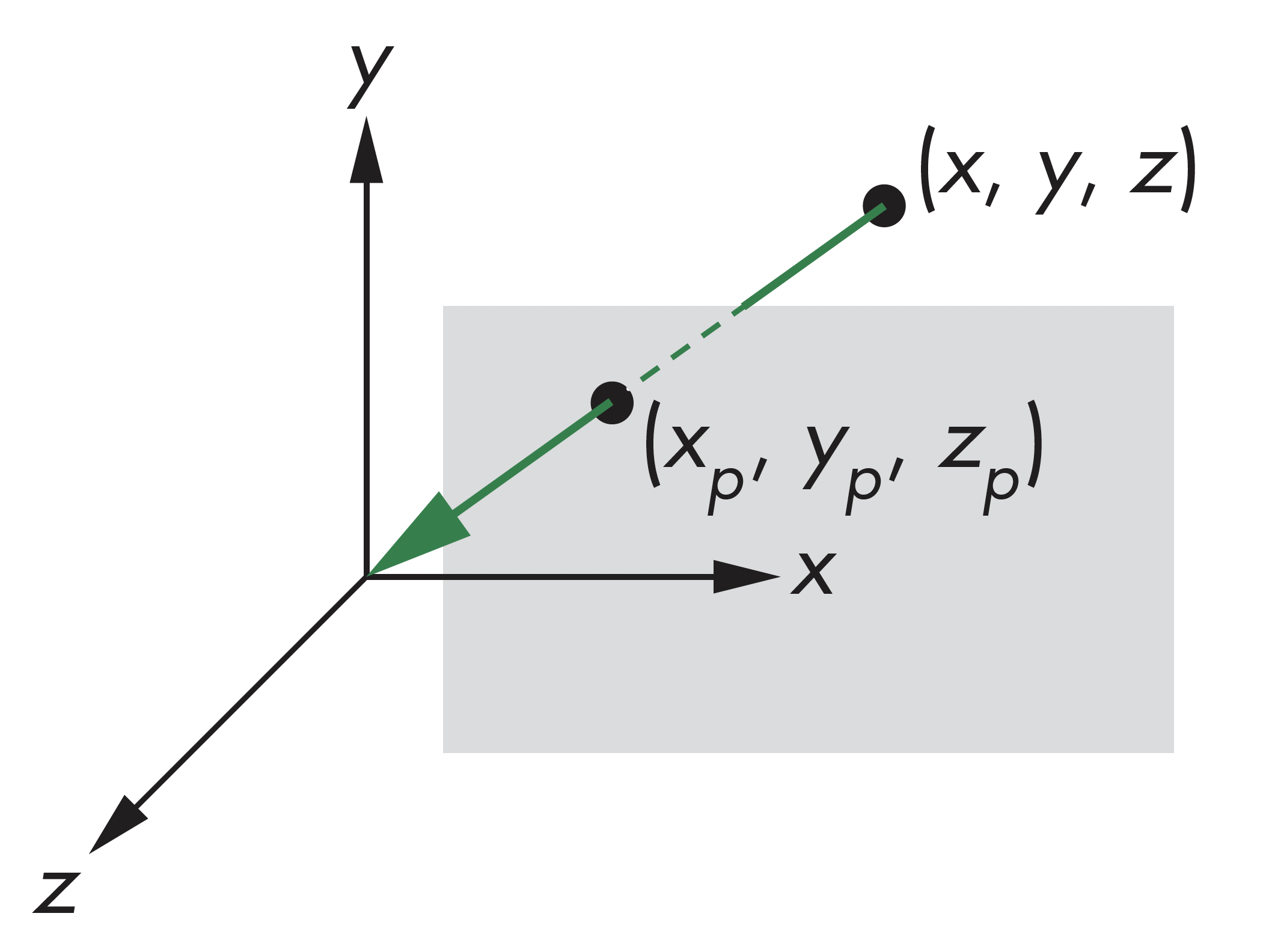
简单透视

投影中心为原点，投影平面位于$z=d,d<0$

投影

投影计算等式

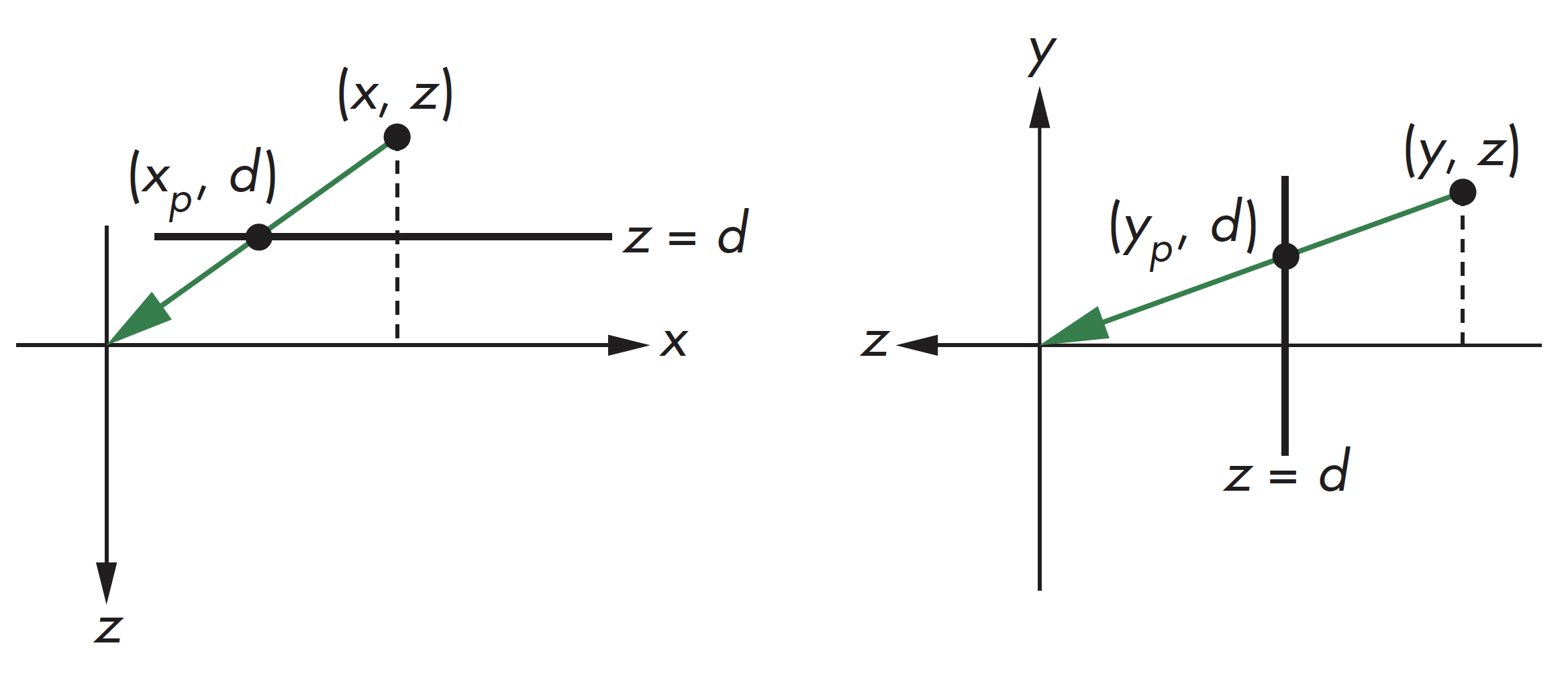
从顶视图和侧视图中计算$x_p,y_p$的值，有 $$ x_p=\frac{x}{z/d}, y_p=\frac{y}{z/d}, z_p=d $$

投影

齐次坐标矩阵形式

同样构建投影矩阵$q=Mp$，其中有$x_p=\frac{x}{z/d}, y_p=\frac{y}{z/d}, z_p=d$， $$ M=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&1/d&0\\ \end{bmatrix} $$
有 $$p=\begin{bmatrix}x\\y\\z\\1\end{bmatrix}, q=\begin{bmatrix}x\\y\\z\\z/d\end{bmatrix}$$

投影

透视因子

• 由于前面式中$q$中$w=z/d\neq 1$，为表达成规范的齐次坐标形式，需要将向量除以$w$
• 因此透视因子为$$x_p=\frac{x}{z/d}, y_p=\frac{y}{z/d}, z_p=d$$

投影

WebGL正投影成像函数

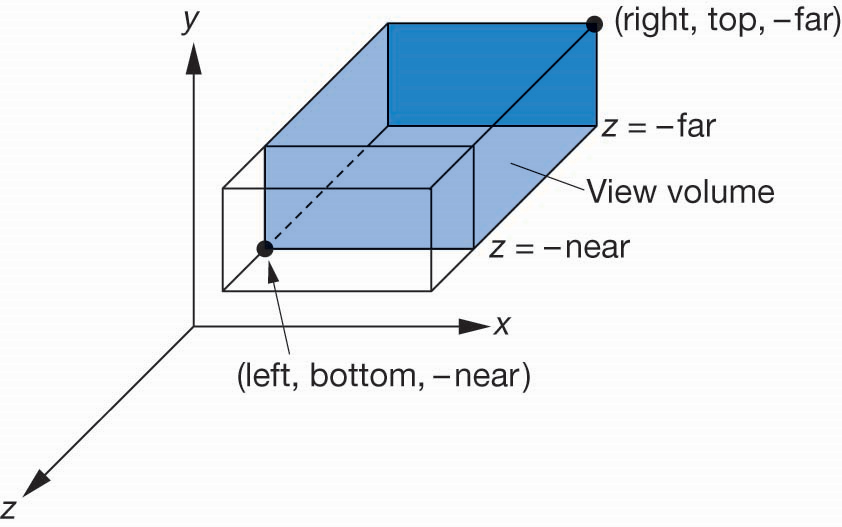
ortho(left, right, bottom, top, near, far)，其中near和far都指的相对相机的距离

投影

WebGL透视投影成像函数

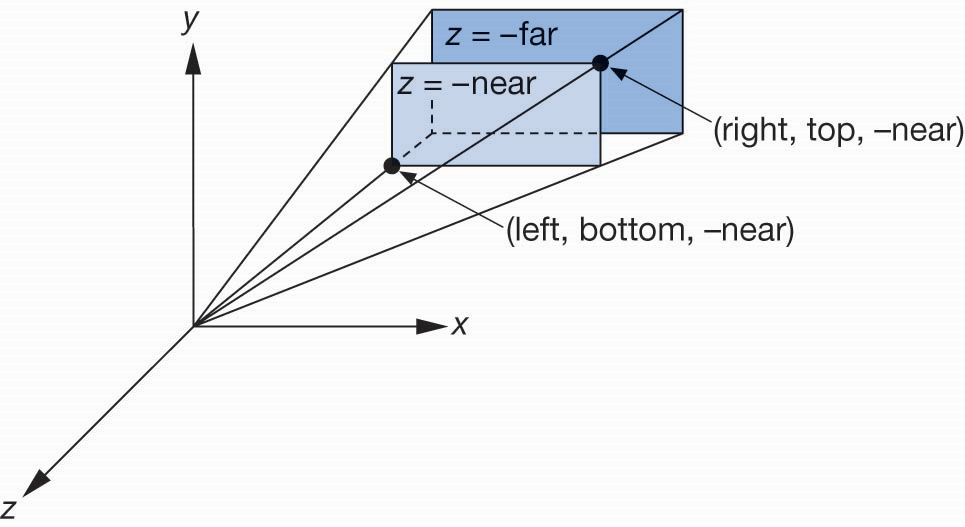
frustuum(left, right, bottom, top, near, far)

投影

视域函数(FOV)

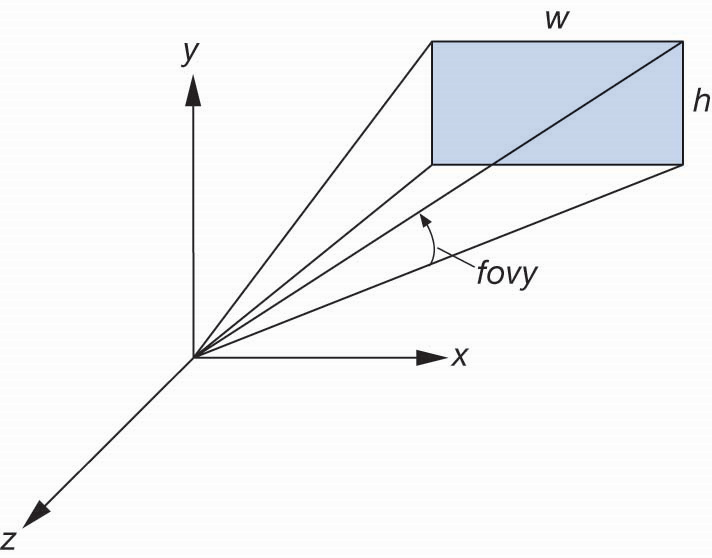
由于用frustum函数一般很难得到准确的成像视图，可选择函数perspective(fovy, aspect, near, far)，能够提供更好的视图构建形式，其中aspect=w/h