计算机图形学
第五章 成像
经典成像
经典成像
何为经典成像
- 成像有三要素
- 成像对象,一个或多个物体
- 观察者,及一个投影平面
- 投影线,将物体投射到投影平面上
- 经典成像建立在这三者间关系基础上,观察者选择对象,选择合适的成像位置和成像方向
- 每个物体对象都可视作是由一系列平面构成,如建筑物、多面体、各种人造物体等
经典成像
平面几何投影
- 标准投影将物体投射到平面成像
- 所有的投影线都是直线,要么平行,要么会聚到投影中心
- 所有的投影线都是直线,能够保持线性关系,但不维持角度大小
- 非线性投影适用于特定的应用,比如地图
经典成像
经典投影示例
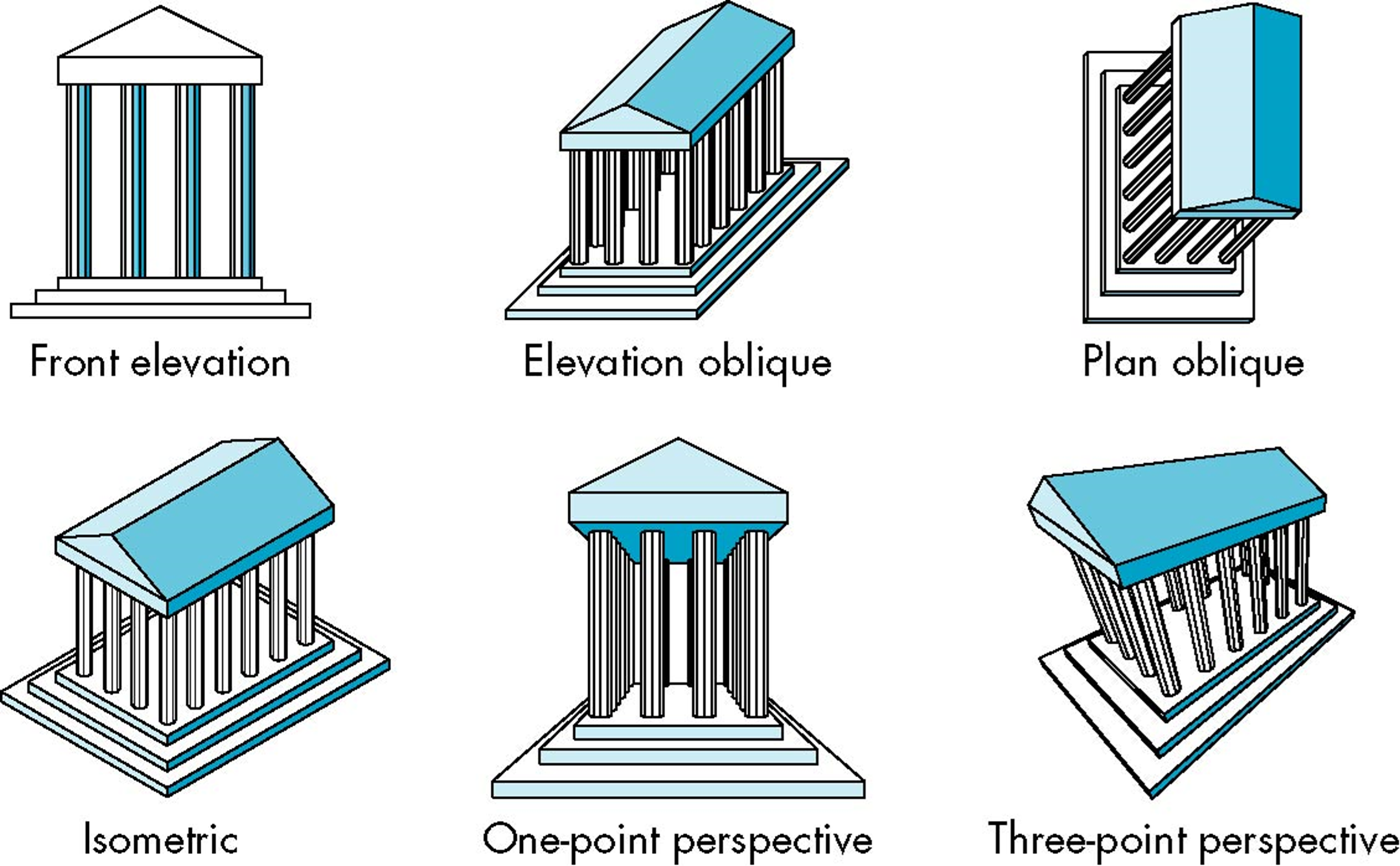
经典成像
平行投影(Parallel Proj.)vs 透视投影(Perspective Proj.)
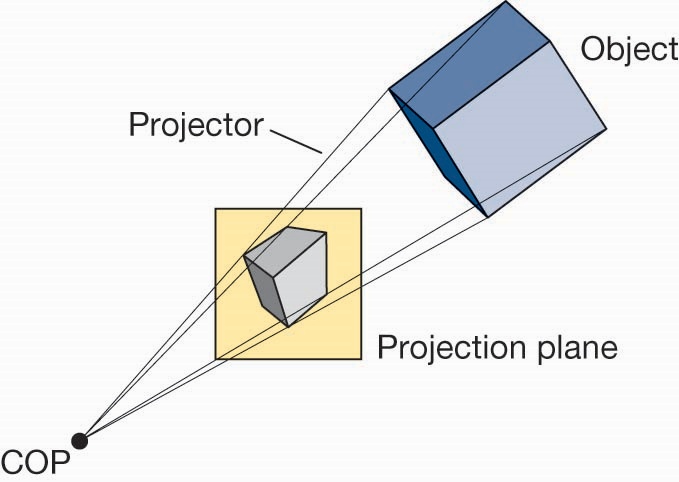
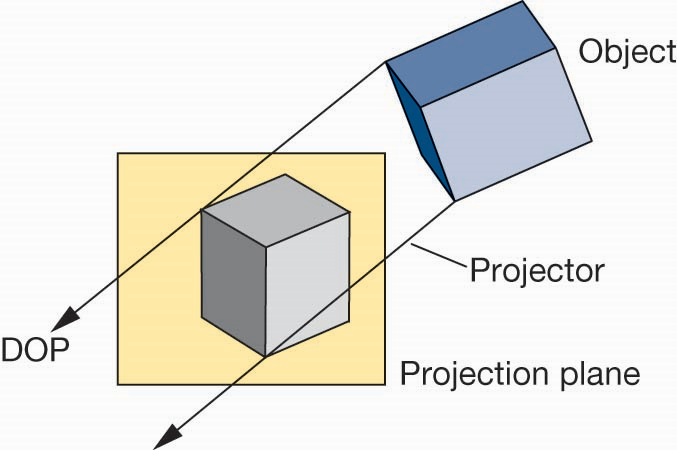
经典成像
投影方式选择
- 经典成像中,两种投影方式的实现是不同的
- 计算机图形学中,所有的成像计算采用同一套管线实现
- 从数学上来看,平行投影是透视投影的极限情况,即投影线的会聚点位于无穷远处
经典成像
平面几何投影分类

经典成像
平面几何投影分类
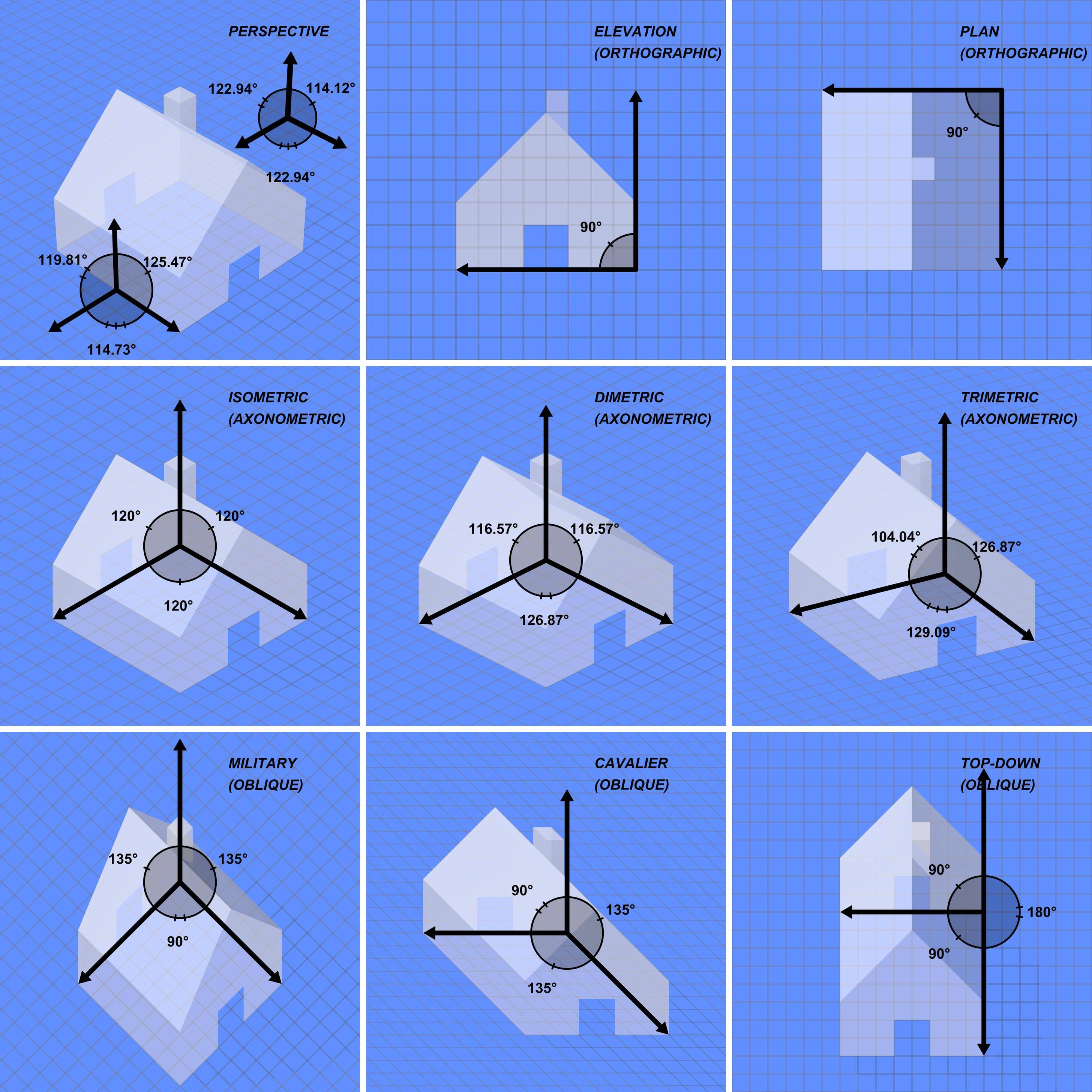
经典成像
正投影(Orthographic Proj.)
- 正投影中,投影线与投影平面垂直
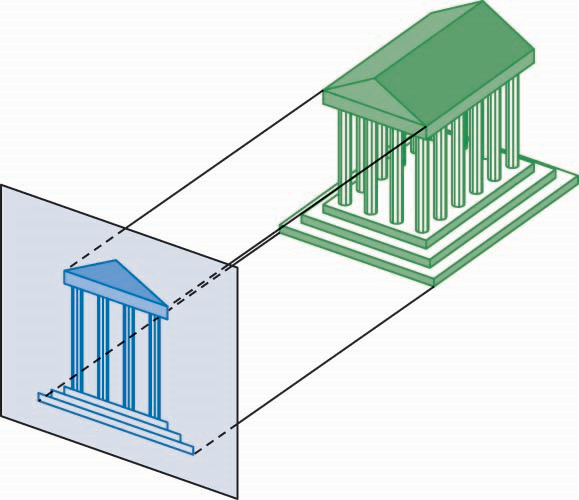
经典成像
多视图正投影(Mutliview Orthographic Proj.)
- 主要投影平面和物体的面平行,一般采用第一人称视图,即正视图、顶视图和左视图
- 一般用于CAD和建筑制图,用三个视图加上等轴测视图构成完整视图

经典成像
正投影优缺点
- 优点:能够保持物体原有的距离和角度
- 维持原有的形状
- 可用于测量,如规划设计、制作手册等
- 缺点:因为视角位置上存在遮挡,无法观察到物体的完整情况
- 通常需要加上轴测图
经典成像
轴测投影(Axonometric Proj.)
投影平面相对物体发生运动
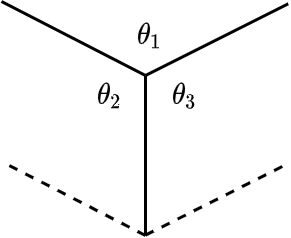
根据投影立方体一角的三个角度几个相同,将轴测投影分为等轴测(isometric, 三个角相同),二轴测(dimetric, 二个角相同),三轴测(trimetric 三个角都不同)
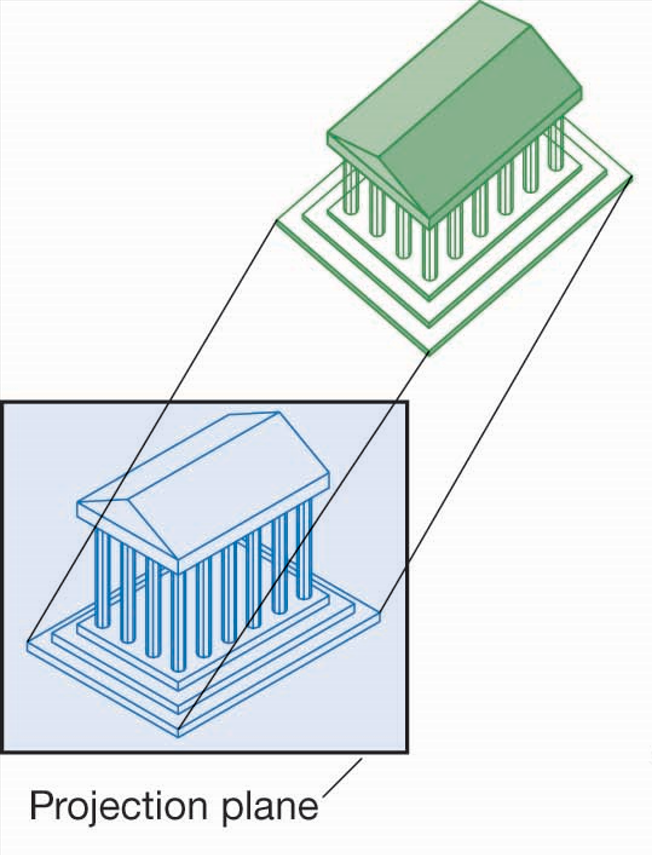
经典成像
轴测投影类型
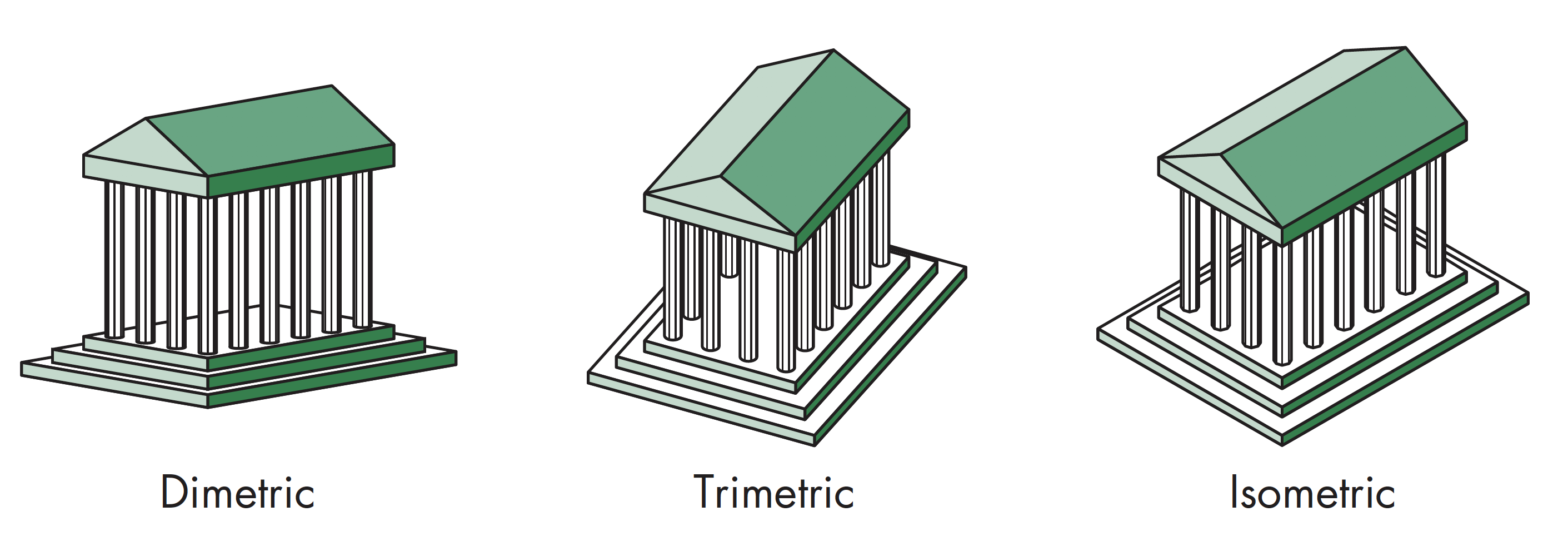
经典成像
轴测投影优缺点
- 线段有缩放, 但能找到缩放系数
- 能够保持线性关系,但无法维持角度关系,如将一个圆投影到不平行的投影平面,形成的结果为椭圆
- 对一个类似盒子的物体,能同时看到三个主要表面
- 可能产生光学错觉,如平行线看起来像发散的线
- 视觉上不具有真实感,远处的物体与近处的物体有同样的缩放系数
- 轴测投影主要用于CAD领域
经典成像
斜投影(Oblique Proj.)
斜投影中,投影线和投影平面之间可以成任意角度
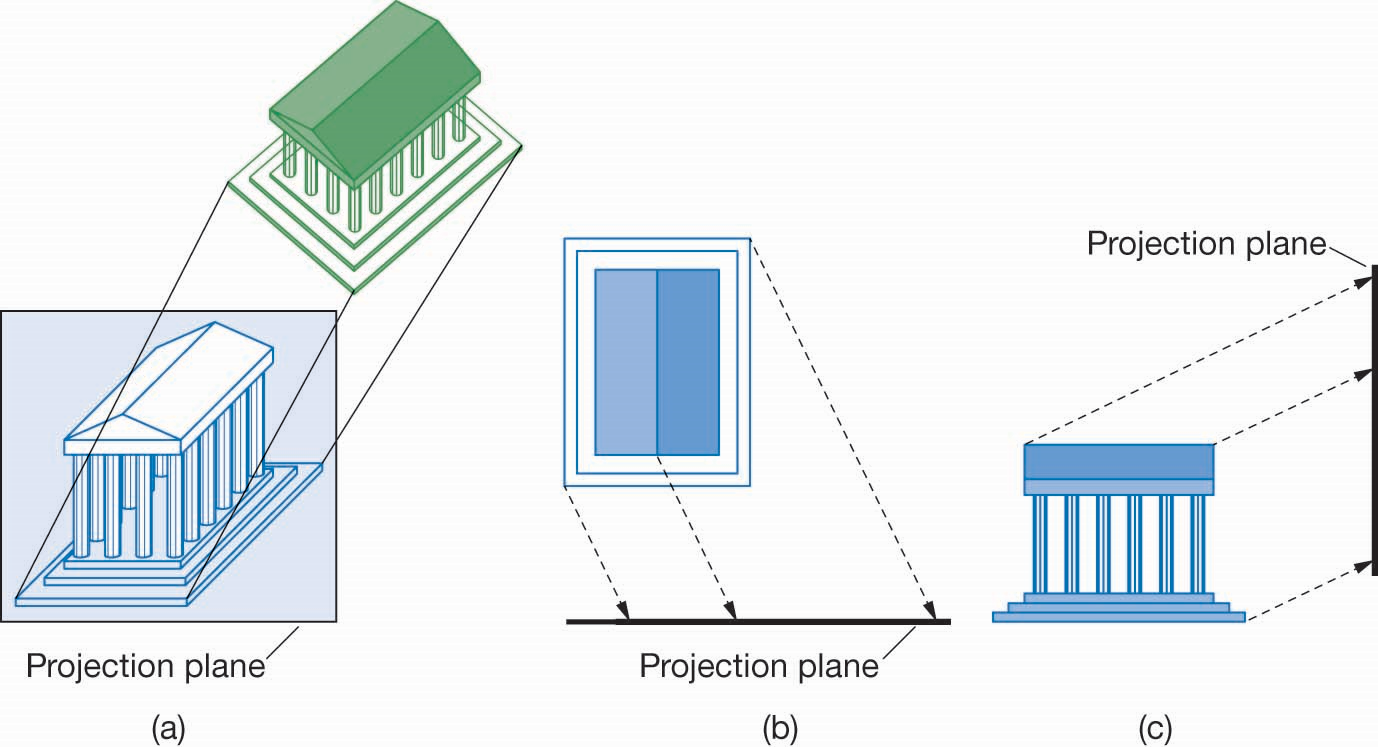
经典成像
斜投影优缺点
- 可选择任意角度,强调物体中某个特定的面,尤其用于建筑设计中
- 与投影平面平行的平面中角度能够维持,同时在斜投影中可以看到周围的面
- 在现实世界中,无法用简单的相机获得斜投影视图,一般需要借助特殊的镜头
经典成像
透视投影
透视投影中投影线会聚到投影中心
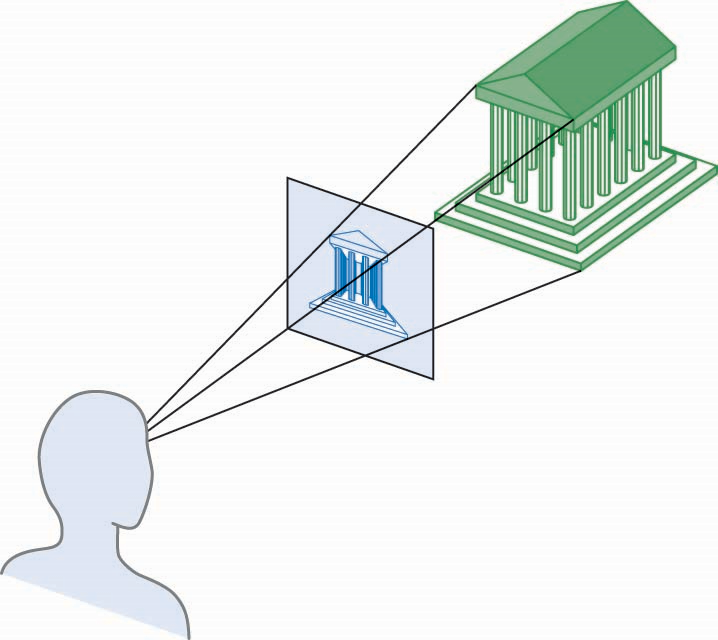
经典成像
灭点
- 物体上的平行线(与投影平面不平行的线)会聚到投影方向上的一点(灭点)
- 利用灭点可以手绘简单的透视投影效果图
经典成像
三点透视
- 三点透视中,没有一个主方向与投影面平行
- 立方体投影有三个灭点

经典成像
二点透视
- 两点透视中,一个主方向与投影面平行
- 立方体投影有两个灭点

经典成像
一点透视
- 一点透视中,两个主方向与投影面平行
- 立方体投影有一个灭点

经典成像
透视投影优缺点
- 距离观察者较远的物体会比距离较近的物体在投影平面上的成像更小,看起来会更真实
- 沿着同一方向两段相同距离的线段在投影成像上距离不同
- 只有与投影平面平行的面上的角度能够得到维持
- 透视投影较难用手绘实现,但计算机中可以