计算机图形学
第四章 几何和变换
齐次坐标
齐次坐标
什么是齐次坐标
如果定义$0\cdot P=0$和$1\cdot P=P$,则可以有 \[v=\alpha_1v_1+\alpha_2v_2+\alpha_3v_3=[\alpha_1\ \alpha_2\ \alpha_3\ 0][v_1\ v_2\ v_3\ P_0]^{T}\] \[P=P_0+\beta_1v_1+\beta_2v_2+\beta_3v_3=[\beta_1\ \beta_2\ \beta_3\ 1][v_1\ v_2\ v_3\ P_0]^{T}\] 可以得到齐次坐标表示,有 \[\mathbf{v}=[\alpha_1\ \alpha_2\ \alpha_3\ 0]^{T}\] \[\mathbf{P}=[\beta_1\ \beta_2\ \beta_3\ 1]^{T}\]
齐次坐标
齐次坐标和计算机图形学
齐次坐标,是计算机图形学中极为重要的概念,表现在如下几方面:
- 所有的标准变换(平移、旋转、缩放)都可用$4\times 4$的矩阵相乘实现
- 硬件流水管线的实现采用的4维的表示
- 对正交投影,对向量,令$w=0$,对点,令$w=1$
- 对透视投影,需要一个透视因子
齐次坐标
改变坐标系
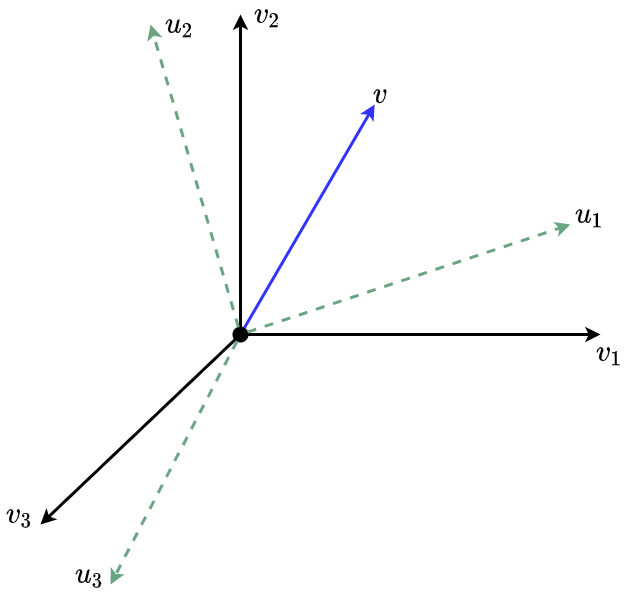
考虑同一个向量,在两组不同的基下有两组不同的表示,分别为 \[\mathbf{a}=[\alpha_1\ \alpha_2\ \alpha_3]\] \[\mathbf{b}=[\beta_1\ \beta_2\ \beta_3]\] 有
\[\begin{aligned} v=\alpha_1v_1+\alpha_2v_2+\alpha_3v_3=[\alpha_1\ \alpha_2\ \alpha_3][v_1\ v_2\ v_3]^{T}\\ =\beta_1u_1+\beta_2u_2+\beta_3u_3=[\beta_1\ \beta_2\ \beta_3][u_1\ u_2\ u_3]^{T}\end{aligned}\]齐次坐标
坐标系表示
第二组基$u_1,u_2,u_3$若用第一组基$v_1,v_2,v_3$表示,有
\[\begin{aligned} u_1=\gamma_{11}v_1+\gamma_{12}v_2+\gamma_{13}v_3\\ u_2=\gamma_{21}v_1+\gamma_{22}v_2+\gamma_{23}v_3\\ u_3=\gamma_{31}v_1+\gamma_{32}v_2+\gamma_{33}v_3 \end{aligned}\]
齐次坐标
坐标系表示
这些参数写成$3\times 3$的矩阵形式有 $$M=\begin{bmatrix} \gamma_{11}\ \gamma_{12}\ \gamma_{13}\\ \gamma_{21}\ \gamma_{22}\ \gamma_{23}\\ \gamma_{31}\ \gamma_{32}\ \gamma_{33} \end{bmatrix}$$ 可进一步写成$$\mathbf{a}=\mathbf{M}^{T}\mathbf{b}$$
齐次坐标
改变标架
对齐次坐标表示的点和向量,也可以进行同样的操作。考虑两个标架$(P_0, v_1, v_2, v_3)$和$(Q_0, u_1, u_2, u_3)$,任何的点或向量都可以在任一标架中表示,因此也就可以用$(P_0,v_1,v_2,v_3)$表示$(Q_0,u_1,u_2,u_3)$
齐次坐标
改变标架(2)
两个标架间,可得到如下表示: $$\begin{aligned} u_1=\gamma_{11}v_1+\gamma_{12}v_2+\gamma_{13}v_3\\ u_2=\gamma_{21}v_1+\gamma_{22}v_2+\gamma_{23}v_3\\ u_3=\gamma_{31}v_1+\gamma_{32}v_2+\gamma_{33}v_3\\ Q_0=\gamma_{41}v_1+\gamma_{42}v_2+\gamma_{43}v_3+\gamma_{44}P_0 \end{aligned}$$ 这样就能得到一$4\times 4$矩阵 $$\mathbf{M}=\begin{bmatrix} \gamma_{11}\ \gamma_{12}\ \gamma_{13}\ 0\\ \gamma_{21}\ \gamma_{22}\ \gamma_{23}\ 0\\ \gamma_{31}\ \gamma_{32}\ \gamma_{33}\ 0\\ \gamma_{41}\ \gamma_{42}\ \gamma_{43}\ 1\ \end{bmatrix}$$
齐次坐标
使用表示
在任意两个标架之间,所有的点和向量都可以用两个标架的基分别表示。有第一个标架$$\mathbf{a}=[\alpha_1\ \alpha_2\ \alpha_3\ \alpha_4]$$ 第二个标架$$\mathbf{b}=[\beta_1\ \beta_2\ \beta_3\ \beta_4]$$ 当有$\alpha_4=\beta_4=1$时为点,当$\alpha_4=\beta_4=0$时为向量,且有 $$\mathbf{a}=\mathbf{M}^{T}\mathbf{b}$$ 该矩阵$\mathbf{M}$是一个$4\times 4$的矩阵,表示齐次坐标的仿射变换
齐次坐标
仿射变换
- 每个线性变换都等价于标架的变换
- 每个仿射变换都能维持线性特征不变
- 仿射变换只有12个自由度,矩阵中其它4个元素是固定的,仿射变换也是所有可能的$4\times 4$线性变换的一个子集
齐次坐标
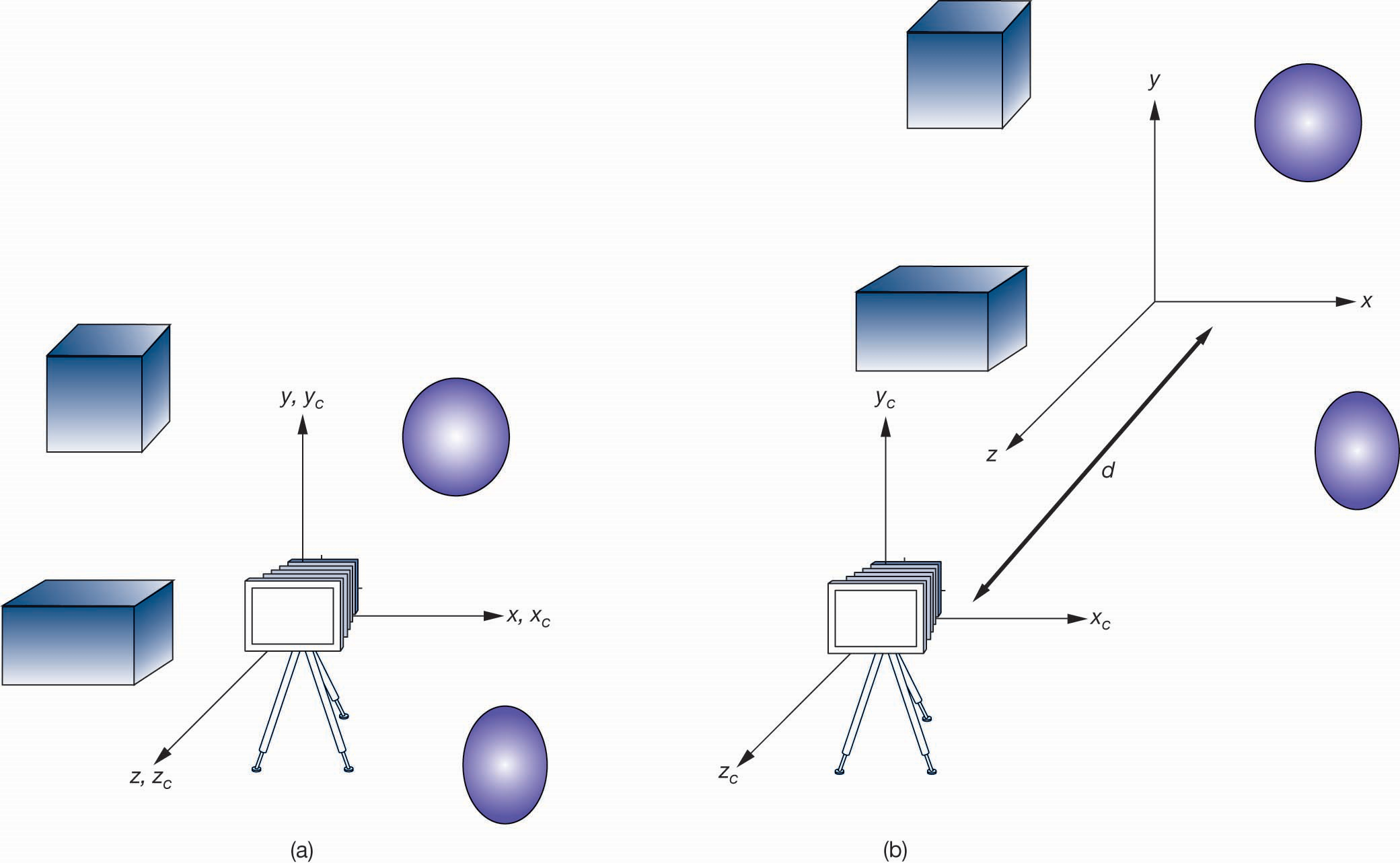
世界坐标系和相机坐标系
- 课程内容中,坐标系和标架会混用,一般用坐标系表示,但要知道指的是标架(Frame)
- 当讨论表示时,讨论的是n元组,或是n维常量,所有的标架变换用齐次矩阵表示,定义为$4\times 4$的矩阵
- 在OpenGL中,最基本的坐标系是世界坐标系,通过模型-视图矩阵,将世界坐标系中的对象变换到相机坐标系中
- 在系统初始化时,所有的坐标系默认都相同,即有$\mathbf{M}=I$
齐次坐标
移动相机
如果在平面$z=0$两侧都有物体,通常需要移动相机到合适的位置